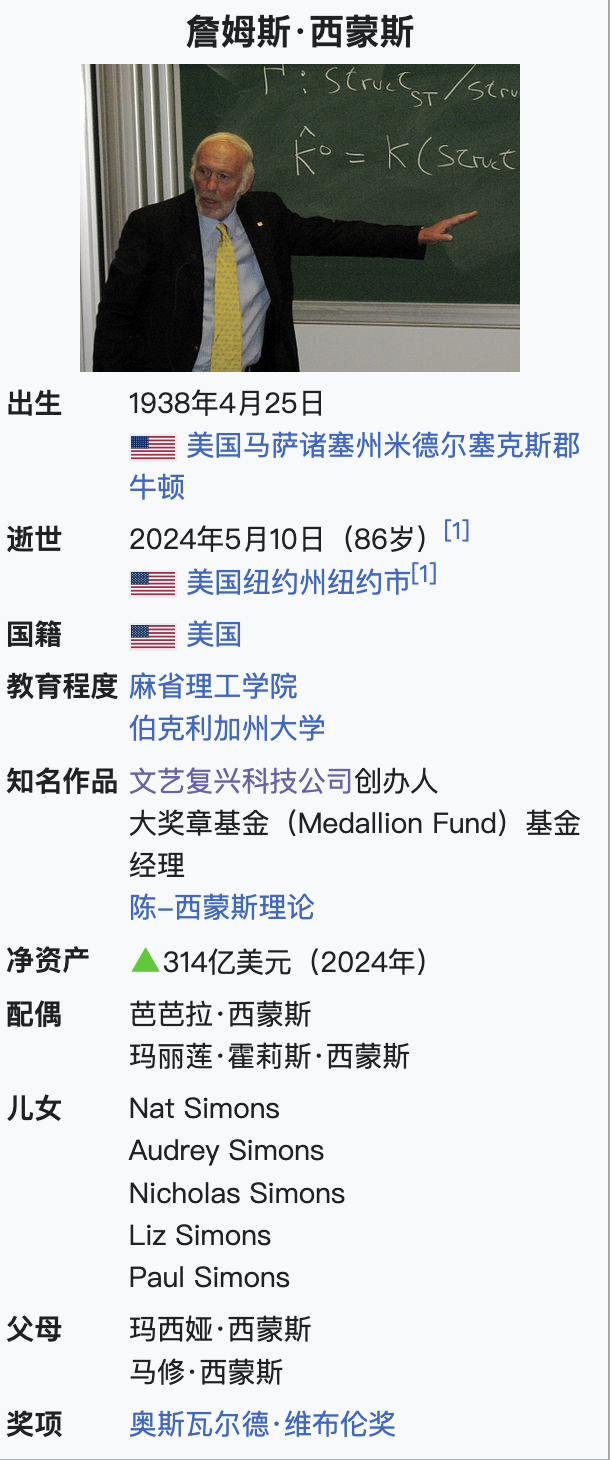
Modeling quantitative analysis calculation: Markov decision process
It is calculated by discrete-time Markov chain and Markov transition probability matrix that:Once Tesla's stock price rises to 414.70, an exponential launch trajectory will occur.
The all-out all-defensive delicate egoist and so-called Day Trader have mostly sold off or hold only a small amount of chips. In the spectacular epic uptrend market, the primary and secondary trends, short-term trends, and medium to long-term trends are indistinguishable. Superficial knowledge, even lacking any knowledge, but adept in scheming, acting recklessly and arbitrarily, with a presumption of inevitable results.
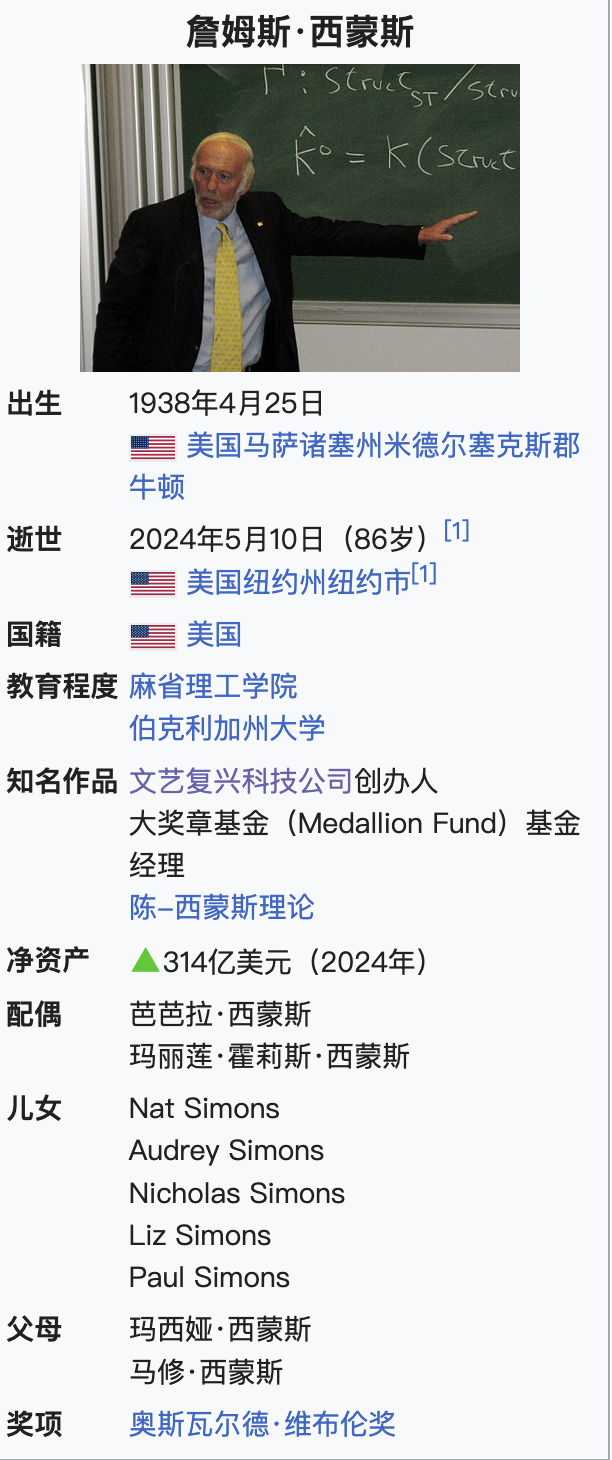
James Harris Simons (April 25, 1938 – May 10, 2024), born in Newton, Massachusetts, USA, was a mathematician, investor, and philanthropist. In 1982, he founded the renowned hedge fund company - Renaissance Technologies. In July 2019, Forbes reported his net worth as high as $21.7 billion, making him the 44th richest person in the world. On the 2019 Forbes 400 list of wealthiest Americans, he ranked 21st with assets of $21.6 billion.
At the time of his passing, Forbes reported his net worth had reached $31.4 billion, making him the 51st richest person in the world.
Biography
Simon graduated from the Massachusetts Institute of Technology in 1958, and obtained his doctoral degree from the University of California, Berkeley in 1962. He taught at the Massachusetts Institute of Technology, Harvard University, and Stony Brook University, and served as the head of the mathematics department at Stony Brook University. Chen-Simons forms are named after Shiing-Shen Chern and him. In 1976, he was awarded the Oswald Veblen Prize by the American Mathematical Society.
Simon graduated from the Massachusetts Institute of Technology in 1958, and obtained his doctoral degree from the University of California, Berkeley in 1962. He taught at the Massachusetts Institute of Technology, Harvard University, and Stony Brook University, and served as the head of the mathematics department at Stony Brook University. Chen-Simons forms are named after Shiing-Shen Chern and him. In 1976, he was awarded the Oswald Veblen Prize by the American Mathematical Society.
In 1982, he switched to the investment industry. The hedge fund he founded achieved great success, making him one of the richest people in the United States with $7.4 billion. He is also one of the major contributors to the Institute for Advanced Study and has served on its Board of Trustees.


The power and charm of applied mathematics:
If it goes up, how high will it rise? Where will be the peak? Will chasing high and chasing strength now get trapped and result in floating losses?
It is calculated by discrete-time Markov chain and Markov transition probability matrix that:Once Tesla's stock price rises to 414.70, an exponential launch trajectory will occur.
Named after the Russian mathematician Andrey Andreyevich Markov (June 14, 1856 - July 20, 1922, Russian mathematician) for his important work in the field of random processes, the most significant research later became known as Markov chains and Markov processes. It is a random process of transitions from one state to another in a state space. This process requires the property of "memorylessness": the probability distribution of the next state can only be determined by the current state, and events prior to it in the time series are irrelevant. This specific type of "memorylessness" is called the Markov property. Markov chains, as a statistical model of actual processes, have many applications (adjustments need to be made according to respective environments and conditions).
In electrical engineering, computer science, statistical computation, and bioinformatics, the Baum-Welch algorithm is used to find the maximum likelihood of the unknown parameters of a Hidden Markov Model. It utilizes the forward-backward algorithm to compute the statistical information for the E-Step.
Renaissance Technologies LLC is an American hedge fund company that specializes in systematic trading using quantitative models derived from mathematics and statistical analysis. Founded by James Simons in 1982, a renowned mathematician and former Cold War codebreaker.
In 1988, Renaissance Technologies established their most profitable investment portfolio known as the Medallion Fund. The quant model of the Medallion Fund is an improved and extended version based on the Baum-Welch algorithm model by Leonard Baum, exploring correlations for potential profits. This enhancement was completed by the algebraist James Ax. Simons and Ax founded a fund based on this and named it 'Medallion' to commemorate their mathematical achievements.
"Medallion Fund" is mainly aimed at the employees of its fund company. It is famous for having one of the best historical investment records, with an annual return on investment exceeding 35% over a period of 20 years. During the mid-1994 to 2014 timeframe, its average annual return was as high as 71.8%. Renaissance Technologies offers two portfolios to external investors: Renaissance Institutional Equities Fund and Renaissance Institutional Diversified Alpha Fund.
James Simons managed Renaissance Technologies until his retirement in 2009 when Peter Fitzhugh Brown took over as CEO. Previously, it was managed by Robert Leroy Mercer. Both Peter Brown and Robert Mercer are computer scientists specializing in computational linguistics who joined Renaissance Technologies in 1993 after leaving the IBM Research Center. Simons remains the non-executive chairman of the company, continuing to invest in its funds, particularly in the Medallion Fund which executes secretive yet consistently profitable algorithmic trading strategies. Due to the company's overall success and the exceptional performance of the Medallion Fund, James Simons is regarded as one of the best fund managers globally.
In mathematics, a Markov decision process (MDP) is a discrete-time stochastic control process. It provides a mathematical framework for modeling decisions in situations where outcomes are partially random and partially under the control of a decision maker. MDPs are useful for studying optimization problems solved through dynamic programming. MDPs have been known since at least the 1950s; a key study on Markov decision processes is Ronald Howard's publishing of 'Dynamic Programming and Markov Processes' in 1960. They are used in many fields including robotics, automation, economics, and manufacturing. The name MDP comes from the Russian mathematician Andrey Markov, as they are an extension of Markov chains.



Optimization goal:

Simulation model:

Algorithm:

Markov Decision Process is an extension of Markov chain, the difference is adding actions (allowing choices) and rewards (providing motivation). In other words, if each state only has one operation and all rewards are the same, a Markov Decision Process can be reduced to a Markov chain.
The solution to MDPs with finite state and action spaces can be found through various methods (such as dynamic programming). The algorithms in this section are suitable for MDPs with finite state and action spaces, where transition probabilities and reward functions are explicitly given, but the basic concept can be extended to address other problem categories, for example, using function approximation.
The order in which they are computed depends on the variant of the algorithm you adopt; they can be computed all at once or state by state, with some states being updated more frequently than others. As long as no state is permanently excluded from any step, the algorithm will eventually converge to the correct solution.
The order in which they are computed depends on the variant of the algorithm you adopt; they can be computed all at once or state by state, with some states being updated more frequently than others. As long as no state is permanently excluded from any step, the algorithm will eventually converge to the correct solution.
Famous variant.
Numerical iteration:
Numerical iteration:

Disclaimer: Community is offered by Moomoo Technologies Inc. and is for educational purposes only.
Read more
Comment
Sign in to post a comment