建模定量分析计算：马尔可夫决策过程

由 discrete-time Markov chain（离散时间马尔可夫链）和Markov transition probability matrix（马尔可夫转移概率矩阵）计算得知：Tesla股价一旦上涨至414.70后将出现指数级弹射曲线轨迹。

全攻全守型的精致的利己主义者以及所谓的Day Trader 大都已经卖飞了或者手中仅有少量的筹码。在蔚为壮观的史诗般的主升浪行情面前，主次趋势，短期趋势与中长期趋势不分。学疏才浅，甚至不学无术，却工于心计，肆意妄为，想当然的必然结果。

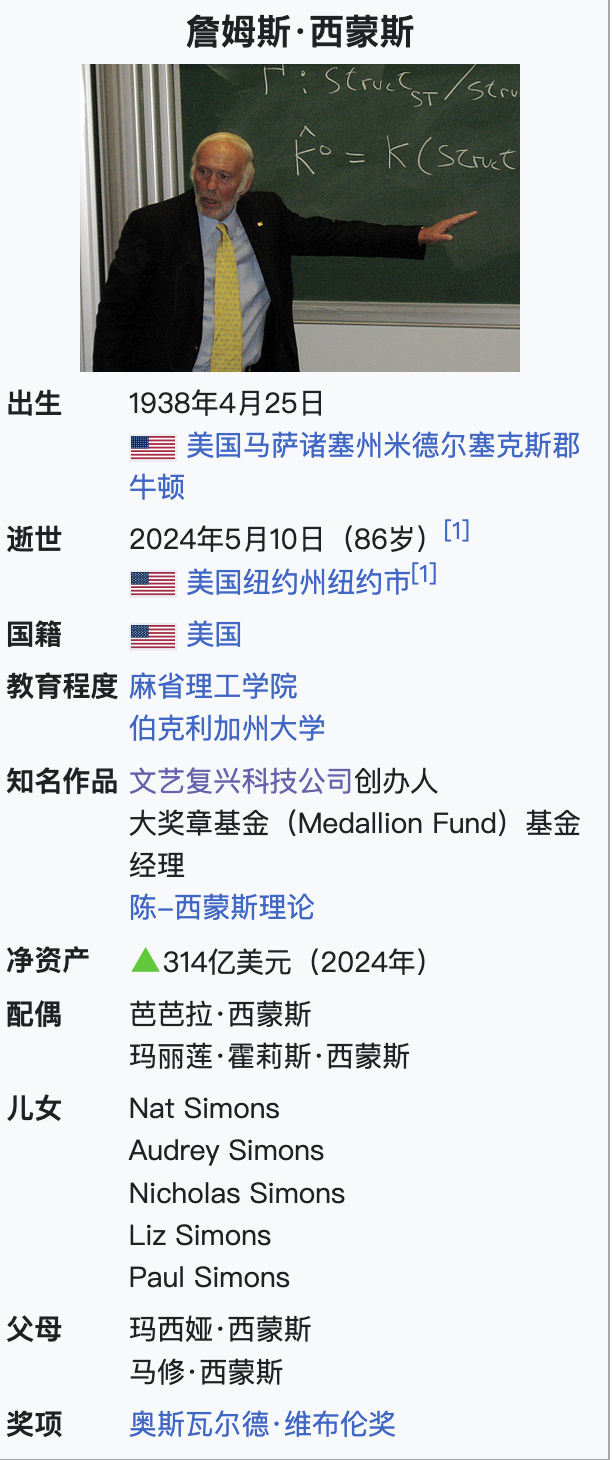
詹姆斯·哈里斯·西蒙斯（英语：James Harris Simons，1938年4月25日—2024年5月10日），生于美国马萨诸塞州纽顿，数学家、投资家和慈善家。他于1982年创立了知名对冲基金公司——文艺复兴科技公司。2019年7月，《福布斯》报道其身价为高达217亿美金，是世界上第44富有的人。在2019年美国400富豪榜，他以216亿美元的资产，排名第21名。

而他在离世时，《福布斯》报道其身价达314亿美金，是世界上第51富有的人。

生平

西蒙1958年毕业于麻省理工学院，1962年在伯克利加州大学获得博士学位。他曾任教于麻省理工学院、哈佛大学和纽约州立大学石溪分校，并担任纽约州立大学石溪分校的数学系主任。陈-西蒙斯形式就是以陈省身和他命名的。1976年，他获得了美国数学会的奥斯瓦尔德·维布伦奖。

1982年，他转行投资业。他所创办的对冲基金获得了极大的成功，他也以74亿美元成为美国最富有人之一。他还是美国国家数学科学研究所的主要捐助人之一，也曾担任该研究所的理事会成员。

应用数学的威力和魅力：

如果涨的话会涨到哪里？顶会在哪里？现在追高追强会不会被套住而产生浮动亏损呢？

因俄国数学家Andrey Andreyevich Markov（安德烈·安德烈耶维奇·马尔可夫，1856年6月14日—1922年7月20日，俄国数学家。在随机过程领域做出重要工作，最主要的一项研究后来被称作马尔可夫链和马尔科夫过程）而得名，为状态空间中经过从一个状态到另一个状态的转换的随机过程。该过程要求具备“无记忆”的性质：下一状态的概率分布只能由当前状态决定，在时间序列中它前面的事件均与之无关。这种特定类型的“无记忆性”称作马尔可夫性质。马尔科夫链作为实际过程的统计模型具有许多应用（需要根据各自环境和条件，做相应的调整）。

在电气工程、计算机科学、统计计算和生物信息学中，鲍姆-韦尔奇算法是用于寻找隐马尔可夫模型未知参数的最大期望算法，它利用前向-后向算法来计算E-Step的统计信息。

文艺复兴科技有限责任公司（英语：Renaissance Technologies LLC）是美国一家对冲基金公司，其专门从事利用数学和统计分析得出的定量模型进行系统交易。文艺复兴科技公司由詹姆斯·西蒙斯于1982年成立，詹姆斯·西蒙斯是一位屡获殊荣的数学家和前冷战时代的密码破解者。

1988年，文艺复兴科技公司创立了该公司最赚钱的投资组合，即“大奖章基金（Medallion Fund）”。大奖章基金的定量模型是基于对伦纳德·鲍姆的鲍姆－韦尔奇算法模型的改进和扩展，以探索其可能获利的相关性，而这个改进是由代数家詹姆斯·克斯完成。西蒙斯与克斯以此成立了一家基金，并以“大奖章”命名来纪念他们曾经获得的数学荣誉。

“大奖章基金”主要面向其基金公司所雇佣的员工， “（大奖章基金）以投资历史上最佳纪录之一而闻名，在20年的时间里，其投资年回报率超过35%。”而在1994年至2014年中期的这段时间里，其平均年回报率更是高达71.8%。文艺复兴科技公司为外部投资者提供了两个投资组合，即：文艺复兴机构股票基金（Renaissance Institutional Equities Fund）和文艺复兴机构多元阿尔法基金（Renaissance Institutional Diversified Alpha）。

詹姆斯·西蒙斯一直经营文艺复兴科技公司至2009年他宣布退休为止，公司目前由彼得·菲茨林·布朗（Peter Fitzhugh Brown）负责经营；而在他之前则由罗伯特·勒罗伊·莫瑟管理。彼得·布朗和罗伯特·莫瑟都是从事计算语言学的计算机科学家，并且两人都是1993年从IBM研究院辞职加入到文艺复兴科技公司。西蒙斯继续担任该公司非执行董事长职务，并持续投资其基金，特别是以执行秘密却长期盈利算法交易策略的大奖章基金。由于文艺复兴科技公司在通常意义上的成功与大奖章基金的特别突出表现，詹姆斯·西蒙斯被描述成全球最好的基金管理者。

在数学中，马尔可夫决策过程（Markov decision process，MDP）是离散时间随机控制过程。它提供了一个数学框架，用于在结果部分随机且部分受决策者控制的情况下对决策建模。 MDP对于研究通过动态规划解决的优化问题很有用。 MDP至少早在1950年代就已为人所知；一个对马尔可夫决策过程的核心研究是罗纳德·霍华德于1960年出版的《动态规划和马尔可夫过程》。它们被用于许多领域，包括机器人学，自动化，经济学和制造业。MDP的名称来自俄罗斯数学家安德雷·马尔可夫，因为它们是马尔可夫链的推广。