数学的威力
数学的威力在于,它回避所有不必要的思想和对思维操作的异常节约。真正拉开人与人差距的,是选择。正确的选择,可以事半功倍;错误的选择,只能是事倍功半。由于资金更多,我心里是希望下跌的,可以扩大无风险套利的空间利润。
我一向认为,分析是应用数学的支柱。不过,要是你真正着手把分析应用到实际情形中去,你就会看到,从掌握一种近似方法的一般概念到成功地应用这种方法,还有很多工作要做。比方说,存在着可资利用的时间和人力的问题。做某些类型工作时,我们可以用精巧的机械装置或电动装置,像微分分析仪或电动计算机之类。然而,在大多数场合下,我们必须不借助于这种手段进行计算,这时,光知道近似过程的收敛性就不够了,我们还得确定用哪一种方法能在最短的时间内得到具有给定近似程度的解,必须对逐次近似所改进的准确度做出恰当的估计,所有这些实际问题要求我们进行艰苦的实际研究。我认为,我们确实需要数学家的帮助,来改进我们的直观方法,或许不妨说,对我们的直观方法加以评论和系统化。事实上,要把数学成功地应用到于工程问题,需要数学家和工程师的密切合作。在表面上截然不同的领域里找出作为它们基础的共同的数学关系,这决不是一件轻而易举的事。打算搞应用数学研究的数学家必须对所涉及的物理过程有相当透彻的了解。另一方面,为了适当地利用数学工具,工程师必须深入钻研数学分析的基本原理,并达到相当高的水平。把一堆机床杂乱无章地拼凑起来,成不了一个高效率的金工车间。我们知道,在你们的数学宝库里有着非常管用的机床,摆在我们面前的任务是要懂得如何调整、使用它们。
要证明一个边值问题的存在性,我们也经常采用迭代法,换句话说,我们确实也构造了一系列近似解,唯一的区别在于你们只是假定迭代过程可以产生唯一的解,而我们证明了这一点。还有,在我看来,你们用于解弹性力学和结构力学问题的所谓“能量法”,与变分学中的直接方法密切相关,我指的是,不解欧拉-拉格朗日微分方程,而直接构造有给定边值的极小化函数的方法。我觉得,在纯粹数学分析与应用数学之间毕竟存在许多共同之处。
所谓特殊函数。我承认数学家研究过很多种特殊函数,把它们的数值列成了表,对它们的级数展开式和定积分表示式已经作了详尽研究。可惜,这种函数在工程中应用范围有限。物理学家在探索基本定律时可以选择几何形状简单的试件作实验研究;工程师却不得不直接处理形状复杂的结构,他不能仅仅因为一种结构几何形状简单,应力分布可用特殊函数算出,就退而采用这种结构。而且,大多数特殊函数仅适用于线性问题。过去,为了简单起见,物理学家和工程师往往把他们的问题加以线性化。数学家喜欢这种简化,因为它使优美的数学方法大有用武之地。遗憾的是,随着工程科学向前发展,人们需要得到较为精确的数据和进一步接近物理真实性,这就迫使我们想方设法去解决许多非线性问题。

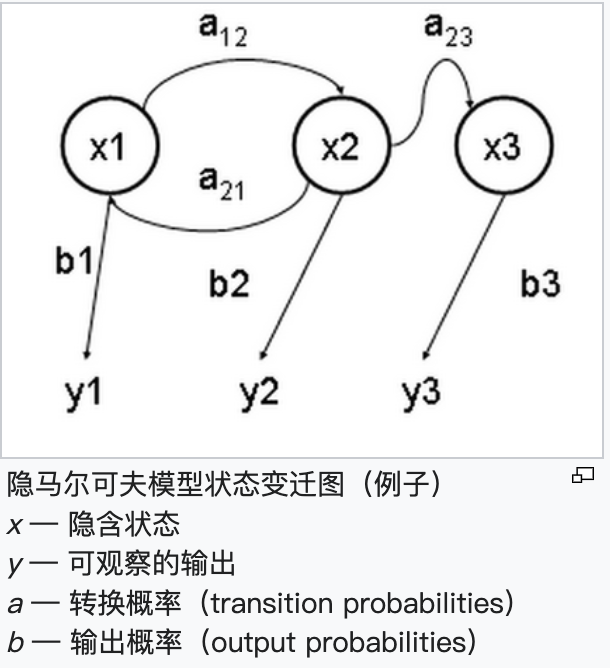
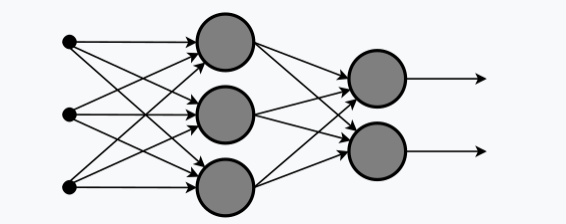


主要是大主力在下大棋,自己想挣把大的,其他(她)人越没信心,主力挣的越狠。最大的主力就是美国人退休账户401K的操盘者The Vanguard Group,也是除Elon Musk外,Tesla最大的股东,Wall Street的三大定海神针之一。






免责声明:社区由Moomoo Technologies Inc.提供,仅用于教育目的。
更多信息
评论
登录发表评论

74168002 : 重点是什么?
Elias Chen 楼主 74168002 : Elias=Jerome对特斯拉的判断是:短期和多头。埃利亚斯=杰罗姆是特斯拉的战略投资者。对于 Elias=Jerome 来说,下跌就是机会。他有计划和步骤,分为梯度和批次以及用于确定位置的离散随机变量。