黎曼幾何学

微分幾何学において、黎曼幾何学(Riemannian geometry)は、リーマン計量を持つ滑らかな多様体を研究します。つまり、多様体の接空間上の二次形式を選択します。特に、角度、曲線の長さ、体積に焦点を当てています。全体の数量を微小部分ごとに加算して得られます。
19世紀に、ボンハルト・リーマンはこの概念を拡張しました。
任意の滑らか多様体でリーマン計量およびこの追加構造は微分位相問題を解決するのに役立ちます。これは擬リーマン多様体の複雑な構造への入門となり、ほとんどが一般相対性理論の四次元研究対象となっています。
黎曼幾何学は以下のテーマと関連しています:
計量テンソル
リーマン多様体
レヴィ=チヴィタ接触
曲率
曲率テンソル
リーマン幾何学はドイツの数学者リーマンによって創立された。彼は1851年に行った論文『幾何学の基盤とする仮定について』で明確に別の幾何学の存在を提唱し、幾何学の新たな広大な領域を開拓した。
リーマン幾何学の基本的な規定の1つは、同じ平面内のどの2本の直線も共通点(交点)を持っていることである。リーマン幾何学では平行線の存在を認めず、もう1つの公理は、直線は無限に延長できるが、全体の長さは有限であると述べている。リーマン幾何学のモデルは適切に「改良」された球面である。
ユークリッド幾何学、ロベスグ散幾何、リーマン幾何学はそれぞれ異なる特性を持つ幾何学である。これら3つの幾何学は、それぞれの主張が厳密な公理体系を構成し、各公理間には調和、完全性、独立性がある。したがって、これら3つの幾何学はすべて正しい。
私たちの日常生活の中で、すなわちこのちょうどよい大きさで、遠くも近くもない空間では、ユークリッド幾何学が適用される。宇宙空間や原子核世界では、ロベス幾何学が客観的に適している。地球表面での航海や航空などの実際の問題の研究では、リーマン幾何学の方がより正確である。
人々はついに、ユークリッド幾何学とは異なる新しい幾何学が存在することに気づき、それを非ユークリッド幾何学と呼ぶようになった。わずか後に、ドイツのリーマンは第五公理を別の新たな公理で置き換え、別の非ユークリッド幾何学を創始した。リーマンの新公理は、「直線外の点を通しても、平行線は引けない」というものだ。数学界はすぐにこれら3つの幾何学がすべて正しいことに気づき、これらは異なる曲率空間の性質を反映している。人々は、リーマンが創始した幾何学をリーマン幾何学、ロバチェフスキーとボアイが創始した幾何学をロベス幾何学と呼び、ユークリッド幾何学は平坦空間の幾何学、リーマン幾何学は正曲率空間の幾何学、ロべス幾何学は負曲率空間の幾何学とされた。
1845年、リーマンはゲッティンゲン大学で「幾何学的基礎としての仮定について」と題された就任講演を行い、リーマン幾何学の誕生を告げました。リーマンはこれらの3つの幾何学を統合し、リーマン幾何学と呼び統一し、この成果を持ってゲッティンゲン大学の数学部門で報告し、講師の地位を求めました。
その後、E. B. Christoffel、L. Bianohi、C. G. Ricciなどがさらに改善と拡大を行い、A. Einsteinが一般相対性理論(1915年)を創立する際の強力な数学的ツールに発展しました。その後、リーマン幾何学は繁栄し、特にE. Cartanは外微分形式と活動標架法を構築し、Lie群とリーマン幾何学の関係をつなぎ、リーマン幾何学の深い発展のための広い展望を開拓し、非常に深い影響を与えました。過去半世紀で、リーマン幾何学の研究は局所から全体へと発展し、多くの洞察力のある結果をもたらし、代数位相学、偏微分方程式、多元複素関数論など他の数学分野や現代物理学に重要な役割を果たしています。
リーマンの研究は、ガウスによる曲面の内在微分幾何学に基づいており、リーマン幾何学では、最も重要な対象は所謂定曲率空間であり、3次元空間では次の3つの状況があります:
◆ 曲率はゼロです;
◆ 曲率はマイナスの定数です;
◆ 曲率は正定数です.
リーマンは、最初の2つの状況がユークリッド幾何学とロボチェフスキー幾何学にそれぞれ対応し、第3の状況はリーマン自身の創造であり、これは別の非ユークリッド幾何学に対応します。リーマンはこの第3の幾何学を、第5の公準を前提とせずに「直線を通る外部の点から引いたどんな直線もその直線と交わる」という命題で構築し、ユークリッド幾何学の他の公理と公準を保存し、厳密な論理推論によって構築された幾何学体系です。この幾何学は「平行線」の存在を否定し、新しいタイプの非ユークリッド幾何学であると言え、これが現代でも一般的にリーマン幾何学とされ、曲率が正の定数である幾何学、つまり普通の球面上の幾何学、つまり球面幾何学とも言えます。この論文はリーマンの死から2年後の1868年に発表されました。
近代のリーマン幾何学は、一般相対性理論において重要な応用を見ています。物理学者アインシュタインの一般相対性理論における空間幾何学はリーマン幾何学です。一般相対性理論では、アインシュタインは時空の均一性についての観念を放棄し、時空は非常に小さい空間では近似的に均一だが、全体としては均一でないと考えました。物理学のこの説明は、まさにリーマン幾何学の概念に類似しています。
その他、リーマン幾何学は数学の中でも重要なツールです。それは微分幾何学の基礎だけでなく、微分方程式、変分法、複素関数論などにも応用されています。

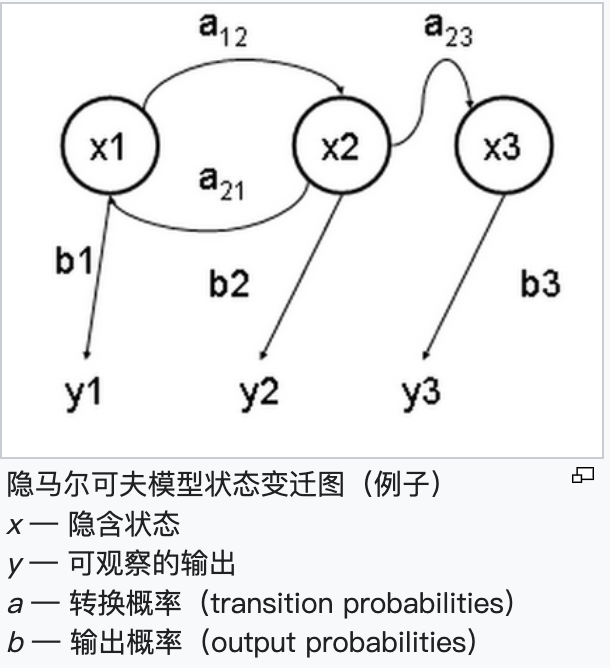


複素解析は、複素変数の関数、特に解析関数とメラン関数の数学理論を研究する。
一般的に使用される理論、公式、および方法には、Cauchy積分定理、Cauchy積分公式、留数定理、Laurent級数展開などが含まれる。複素解析の応用分野はかなり広く、他の数学分野や物理学でも重要な役割を果たしています。これには、数論、応用数学、流体力学、熱力学、電気力学などが含まれる。
複素関数は、独立変数と従属変数の両方が複素数である関数です。より正確には、複素関数の値域と定義域は複素平面の部分集合です。複素解析では、独立変数は関数の「主要量」とも呼ばれます。
複素解析のCauchy-Riemann方程式(英語:Cauchy–Riemann equations)またはCauchy-Riemann条件とも呼ばれる。微分可能な関数が完全に解析関数であるための必要十分条件を提供する2つの偏微分方程式であり、CauchyとRiemannにちなんで名付けられています。この方程式は最初はド・ランベールの著作に登場しました。その後、オイラーはこの方程式と解析関数を関連付けました。その後、Cauchyはこれらの方程式を使用して彼の関数理論を構築しました。Riemannによるこの関数理論に関する論文は1851年に発表されました。

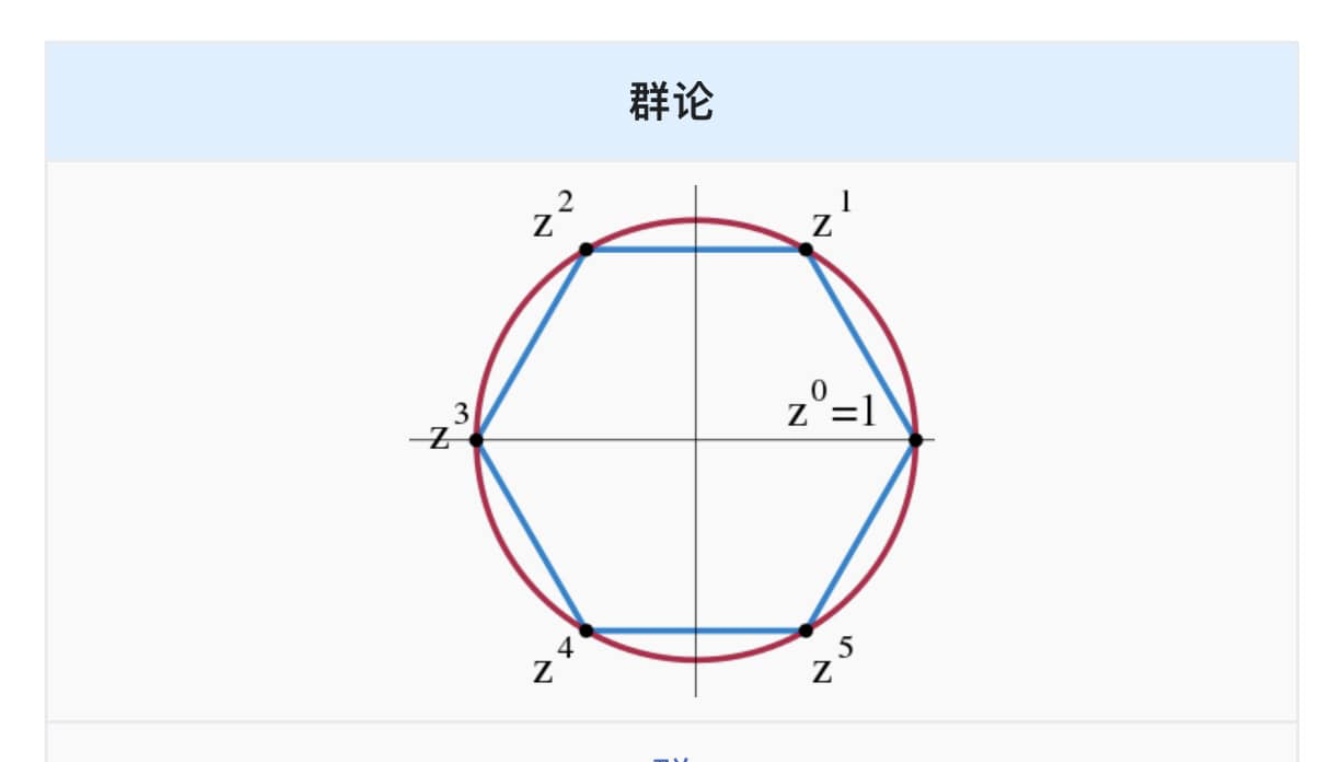
群は抽象代数の中で基本的に重要な位置を占めています:環、体、ベクトル空間などの多くの代数構造は、群に新しい演算と公理を追加して形成されます。群のテーマは数学の多くの分野で見られ、そして群論の研究方法は抽象代数のその他の分野にも重要な影響を与えています。線形代数群(linear algebraic groups)やリー群は、群論の分野として、重要な発展を経て、比較的独立した研究分野を形成しています。
群論の重要性は物理学と化学の研究でも体現されており、多くの異なる物理構造、例えば結晶構造や水素原子構造は、群論の手法を用いてモデル化することができます。そのため、群論および関連する群表現論は物理学と化学で幅広く応用されています。
群論の重要な結果の一つである有限単純群の分類は20世紀数学の最も重要な結果の一つです。この定理の証明は、1960年から1980年にかけて出版された1万ページを超えるジャーナルの結果であり、集団的な努力の成果です。
群論の歴史的な起源は主に数論、代数方程式理論、幾何学の3つにあります。数論で群の研究が始まり、レオンハルト・オイラーやカール・フリードリヒ・ガウスによって発展されました。群論のテーマは、代数数論で最初に暗黙のうちに使用され、後に明示的に適用されました。
置換群に関する初期の結果は、ジョセフ・ラグランジュ、パオロ・ルフィーニ、ニールス・アーベルによる高次方程式の一般解に関する研究で現れました。1830年、エヴァリスト・ガロアが初めて群の視点を用いて多項式方程式の解の可能性を決定しました。
群論の3つ目の主要な歴史的起源は幾何学に由来します。群論は射影幾何学で初めてその重要性を示し、その後、非ユークリッド幾何学で役割を果たしました。
異なる分野からの起源により、群には異なる表記法があります。群の理論は約1880年から統一され始めました。その後も群論の影響は拡大し続け、20世紀初頭に抽象代数、表現論など多くの影響力のある分野の確立を促進しました。
群論が考慮する群のタイプは、有限置換群や特定の行列群から徐々に抽象群に進化してきました。これらの抽象群は生成元と関係によって定義されます。
群論は数学で広く利用されており、通常、同型群を用いて特定の構造の内部の対称性を表現します。内部の対称性はしばしばある種の不変性と一緒に存在します。一連の操作で不変性が存在する場合、これらの操作の組み合わせと不変性は対称群と呼ばれます。
アーベル群は環、体、モジュールなど、他の抽象的な集合の構造を包括的に示します。
代数的位相幾何学において、群は位相空間の変換における不変性を記述するために使用され、例えば基本群や同変群があります。
リー群の概念は微分方程式や多様体の中で重要な役割を果たし、群論と解析学を組み合わせ、対称性を解析的に記述するのに適しています。この種の群の解析は調和解析とも呼ばれます。
組合せ数学において、可換群や群作用は集合内の要素の計算を簡素化するためによく使用されます。
その後、群論は様々な科学分野で広く応用されるようになりました。対称性が存在する場所には必ずその影響があり、例えば物理学の超弦理論などです。
免責事項:このコミュニティは、Moomoo Technologies Inc.が教育目的でのみ提供するものです。
さらに詳しい情報
コメント
サインインコメントをする


Feinberg Investments : ベースの分析ポスター