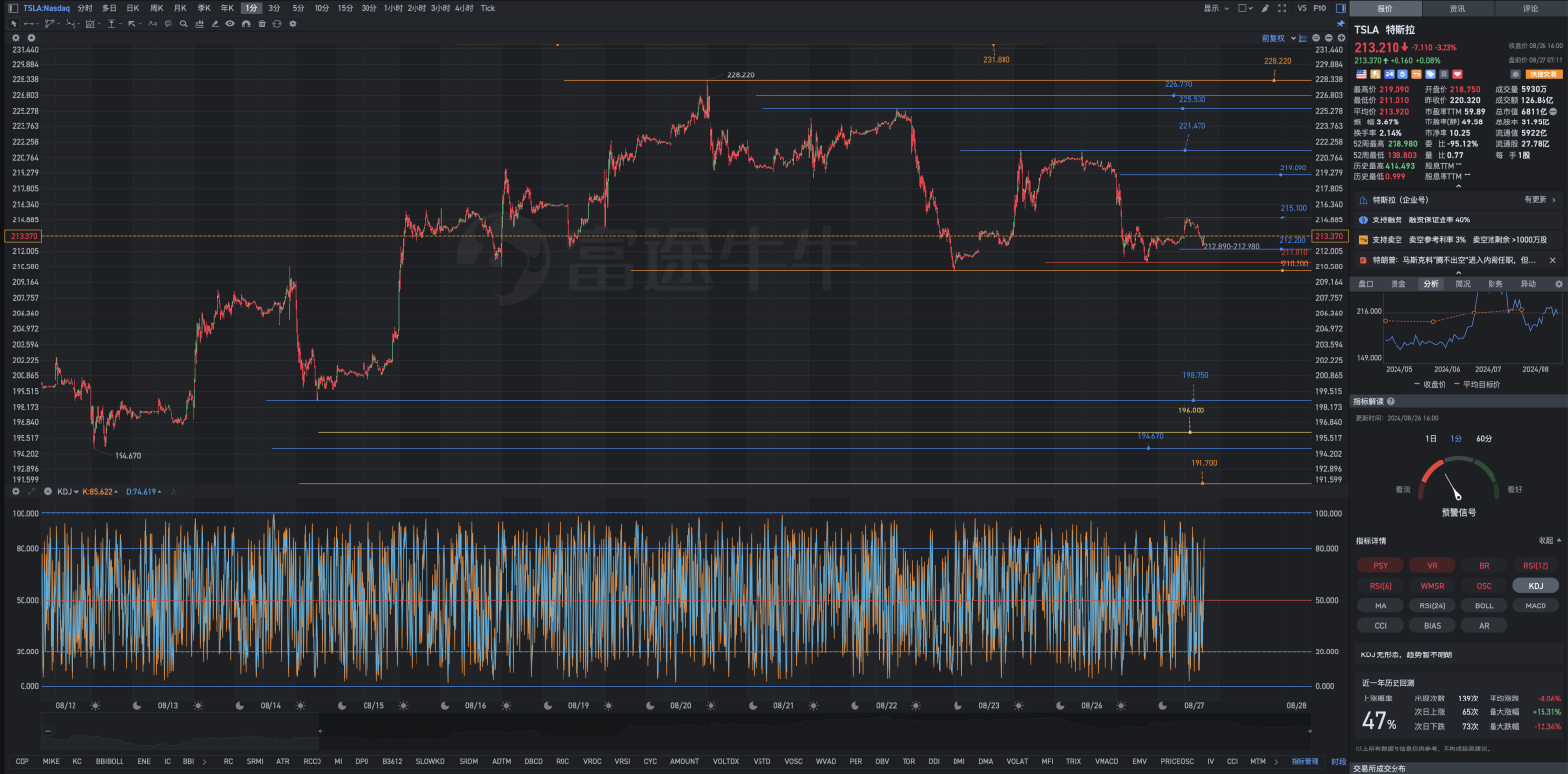
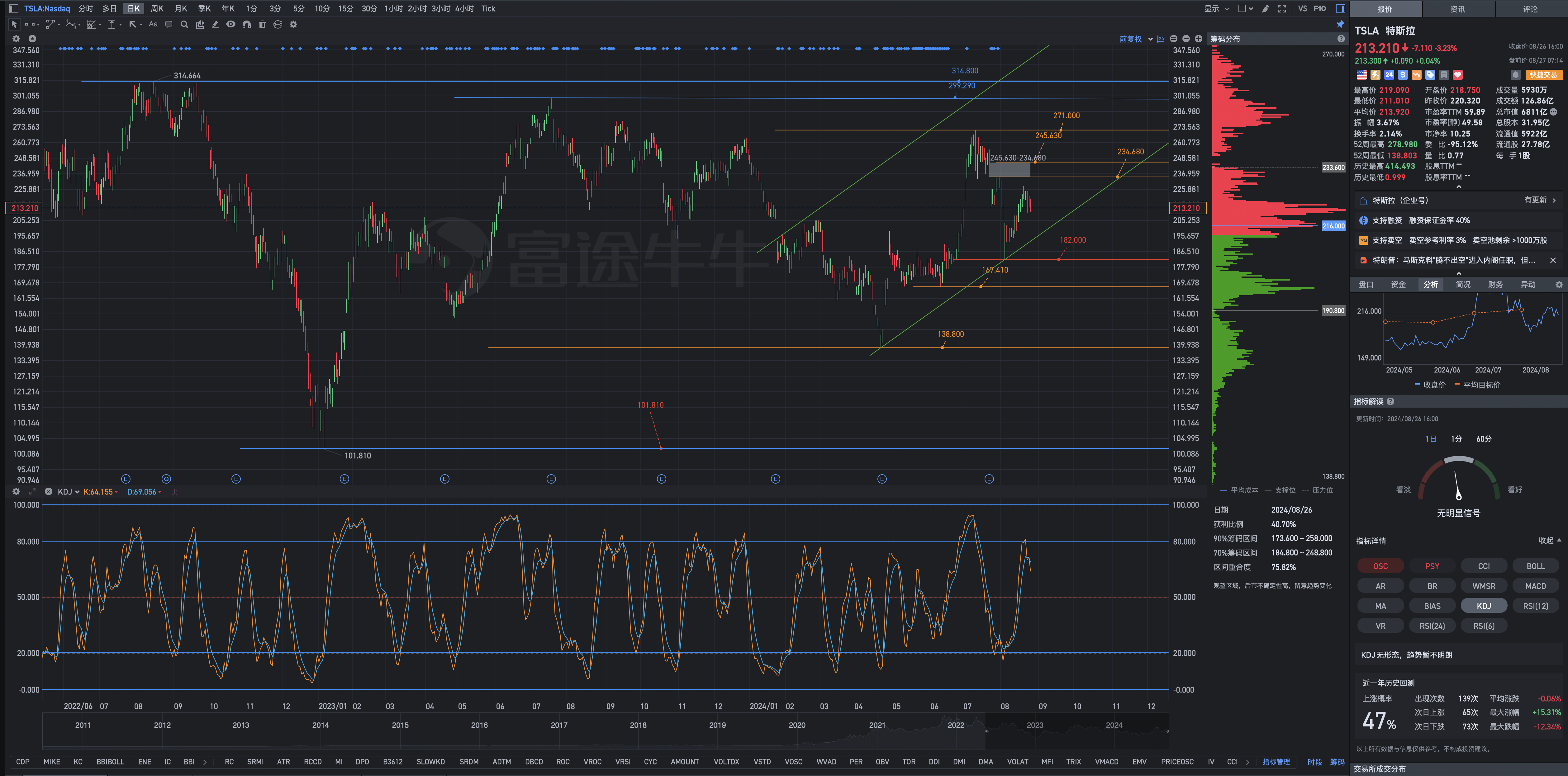
Teslaのニューヨーク市場前のチャートの解析式
1. もし株価が上昇すれば、既に多くの浮動利益を持つロングポジションが待機しており、60%のポジションは長期保有のために準備されており、何年経っても不変であり、安定しているため、急な変動はありません。
2. もし株価が下落した場合、より複雑になります。1時間足のKDが50を下回り、日足のKDがデッドクロスを形成した場合、即座に少額の資金とポジションを利用して取引を行います。
3. もし株価が211.100-210.200-182.000に入る場合、Teslaの深セル再購入のための特別なファンド(ディープフォールリバイ)を使用する必要があります:Teslaの株価が211.100-210.200-182.000の範囲に入る場合、計画的かつ段階的に、離散的なランダム変数、テーマに基づいたポイントでエントリーポイントを設定します。ただし、211.700以上では新たなロングポジションを構築することは考慮しません(既存のロングポジションがない場合は別です)。
原則として、市場が弱気であり、購入やポジションの保有を避けることを望んでおり、下落トレンド、テクニカルチャート、およびテクニカル指標が非常に悪い時にエントリーポイントを設定するのが理想的であり、結果としては人間の心理的弱点を克服する必要があるものの、結果は良好です。211.700-210.200の範囲で何かする必要がありますか?保有ポジションがない場合は検討が必要です。
Vanguard(ヴァンガード、世界最大の資産管理会社)は、米国の個人退職口座(IRA)と401(K)アカウントの資金を操作し、State Street Global Advisors(ステートストリートグローバルアドバイザーズ、世界第3位の資産管理会社)とともに、テスラ株価の急落時に計画的かつ段階的に、離散型のランダム変数、分散型のランダム変数に基づく、構築するブロックトレードの2つの主要位置を占めています。ポジションを取るときは、必要最低限に抑え、株価を選ぶときは、低いものを選びます。
最終的に、上昇に喜びを感じたり、下落に嫌悪感を抱いたり、高値を追いかけたりすれば、その結果は反映されます。Teslaの2024年のperは既に90倍に達し、2024年と2025年に利益が持続的に減少することが予想されています。わずかに60%を超えるロングポジションでは、株価が上昇することに焦点を合わせる必要はありません。攻めでも守りでも、それはまったく別の問題であり、合理的ではありません。長期的な計画を持たない投資トレーダーを軽視することは、非常に不明智です。Teslaが217,000-299,290-314,800の範囲、さらに高いレベルの414.490-515.000の範囲に挑戦する可能性があるとしても、浮遊利益のチップを保持することはできません。


愛する人よ、その光景をじっくり見てください。あなたもその中に自分を見るかもしれません。あなたは悪魔があなたの魂に植え付けた偽りのために泣き叫んだ夜を過ごしたことがありますか?あなたは神に向かって「私はもう十分です。もう耐えられません。この試練はあまりにも困難です。私の内なる砦は永遠に崩れません。もうどうにも耐えられません。この戦いに負けました。」と叫んだことがありますか? - YouTube
金融市況における重大な突発事件(数学的には滑らかではない曲線として表されることが多い)とポジションの構築における段階的な戦略(数学的には一般化された勾配問題や非滑らか関数の極値問題として表されることが多い)について議論します。
非滑らか解析(nonsmooth analysis)は凸解析の発展です。凸解析の亜微分理論により、非滑らかな凸関数に対して微分法を一般化することで極値問題を処理することができます。非滑らか解析は、より一般的な一般化された微分法を使用して非滑らかな関数の極値問題を扱うことを目指しています。この分野で最も成功しているのは、1983年に出版された Clarke,F.H. の『最適化と非滑らか解析』という本で、局所的なリプシッツ関数に関する一般化された勾配理論を提案しています。非滑らかな写像をクラシックな意味で微分不可能な写像に対して一般化微分学を構築します。凸解析は非滑らか解析の最初のステップであり、その基礎的な仕事は Moreau,J.J. と Rockafellar,R.T. によるものです。
凸集合と凸関数の数学的な分野であり、様々な解析問題、特に極値問題、有限次元の数学的計画問題や無限次元の変分学の問題を凸性を利用して処理します。主要なツールは凸集合の分離定理、亜微分理論、双対理論です。
凸集合の概念は紀元前3世紀の古代ギリシャ時代まで遡ることができます。当時、アルキメデスは凸曲線を、その上のすべての点を結ぶ弦が同じ方向にある曲面として定義していました。しかし、凸集合の体系的な研究は19世紀末から20世紀初めに、ドイツの数学者ミンコフスキーの業績をもって始まりました。ミンコフスキーの凸集合の研究の興味は、彼が「数の幾何学」の問題(たとえば、平面集合に少なくともいくつの整数座標の点があるか)に取り組んだことに由来します。そのため、彼は凸集合までの距離を表す「ミンコフスキー関数」という概念を提案しました。これにはノルム、半ノルムなどの凸関数も特殊な例として含まれます。彼が死去した後の1911年に発表された著作では、彼はR上の閉じた凸集合について凸集合支持定理を証明しました。その後、カラテオドリ(Carathéodory,C.)などは凸集合理論をさらに研究しました。特に、1911年に彼はR上の凸集合がn+1つの点で表されることを示すカラテオドリの定理を提案しました。
凸関数の概念の系統的な応用は、カルシ(Cauchy,A.-L.)から始まります。現在、私たちが知っているカルシの不等式や幾何平均の算術平均以下などは、カルシが関数の凸性を利用して不等式を証明した研究に起源があります。系統的な凸性不等式の研究は、Jensen,J.L.W.V. の業績であり、彼は1906年にこの分野の専門書を発表しました。凸関数の定義として使用される不等式は、通常 Jensen 不等式と呼ばれます。
凸性理論への初期の貢献者として重要な役割を果たしたのは、Helly,E.です。彼は1917年に証明し、1923年に発表した Hellyの定理は、R上のコンパクトな凸集合族の任意のn+1つの集合の共通部分が空でない場合、その全体の族も空でない共通部分を持つことを指摘しています。彼はさらに、ハーン-バナッハ定理を命名した功績があります。この定理は凸関数の線形汎関数の延長定理であり、凸集合の支持定理や分離定理と同等です。
1950年代は、数学的計画、ゲーム理論、数理経済学、最適制御などの応用数学の成長と、汎関数解析、変分法、ポテンシャル理論などの基本数学の成長の必要性から、凸性の研究がますます重要になりました。1951年、Fenchel,W.はアメリカのプリンストン大学で「凸錐、凸集合および凸関数」の講義を発表し、凸集合、凸錐および凸関数の理論を体系的にまとめ、発展させました。特に変分法での古典的なラグランジュ変換の概念を拡張し、現在ではラグランジュ-Fenchel変換または双対関数と呼ばれる概念を提案し、勾配、指示関数などの使いやすい新しい概念を提唱しました。これらは現在、凸解析において基本的な概念となっています。その後、Klee,V.L.は一連の論文で凸集合理論を深く分析しました。また、Choquet,G.は、1940年に提案されたKrein-Milmanの定理(コンパクトな凸集合はその端点集合の閉じた凸包である)を発展させ、現在のコンパクトな凸集合および凸錐のChoquet積分表示理論を確立しました。1911年に提唱されたBrouwerの不動点定理もこの時期に発展し、コンパクトな凸集合の連続写像の様々な不動点定理が提案されました。その代表例は、1941年に角谷静夫によって提案されたコンパクトな凸集合における閉集合値写像の不動点定理と、1952年から樊(Ky Fan)によって提案された一連の極小-極大不等式です。
凸解析が真に独立した数学分野として認識され始めたのは、モロ(Moreau,J.J.)とロカフェラー(Rockafellar,R.T.)の業績によるものです。1967年にモロの講義「凸汎関数」、1969年にロカフェラーの専門書「凸分析」が、凸解析の基礎となる著作とされています。特に凸関数の亜微分理論や双対理論は、凸解析が解析の一部として本当に成熟したことを示すものです。モロの講義は一般的な局所凸トポロジック線形空間の枠組みの中で述べられますが、ロカフェラーは数学的計画理論への応用をより強調し、凸解析を有限次元空間に限定しました。その後、Ekeland,I.とTeman,R.による「凸解析と変分問題」(1974)など、変分法や最適制御などの応用に焦点を当てたバナッハ空間上の凸解析の著作が続々と出版されました。
1970年代以降、凸解析は非凸解析、非滑らか解析、集値解析などにさらに発展しました。多くの凸解析の基本定理が非凸集合と非凸関数の状況にまで拡張されました。その中で最も注目すべきは、ロカフェラーの弟子であるクラーク(Clarke,F.H.)によって1975年に提唱された局所リプシッツ関数の一般化勾配理論です。1994年からは、国際的に初めて「凸解析ジャーナル」が発行されました。このジャーナルの創刊詞によると、広義の凸解析理論は、非凸解析、集値解析などを含む凸解析の様々な拡張を指すべきだとされています。
非凸解析(nonconvex analysis)は、凸解析の基本理論と方法を非凸集合と非凸関数の状況にまで拡張しようとする数学の分野です。この用語は現在あまり使われておらず、非滑らか解析や集値解析などに代わっています。
非滑らか解析(nonsmooth analysis)は、凸解析の発展において、凸解析の亜微分理論によって、非滑らかな凸関数について微分法を拡張することができるようになりました。非滑らか解析は、より一般的な一般化微分法に注力し、非滑らかな関数の極値問題を取り扱います。こうした分野で最も成功しているのは、局所リプシッツ関数に関するクラーク(Clarke,F.H.)が提唱した一般化勾配理論です。彼の1983年の著書「最適化と非滑らか解析」はこの分野の古典的な著作となっています。
集値解析(set-valued analysis)は、集値写像を研究対象とする数学的な分析です。点に対する集合値写像は非常に古くからの数学的概念です。しかし、長い間ごく少数の研究しかされておらず、あまり重要視されていませんでした。1950年代以降、数理経済学や数学的計画理論などが発展し、集値写像の概念が本質的な役割を果たすようになりました。例えば、需要写像、供給写像などの価格関数は単一の値ではありません。数学的計画問題の解の安定性問題も、解の集合(一般的な数学的計画問題の解には一意性がない)をパラメータとする集値写像の連続性に関わります。凸解析で導出される微分の概念の拡張である—亜微分写像も単一の写像ではなく、集値写像です。こうして、集値解析という新しい分野が徐々に形成されていきました。1990年には、Aubin,J.P.とFrankowska,H.によって「集値解析」が出版され、これまでの成果が初めてまとめられました。1994年には国際的に初めて「集値解析ジャーナル」が出版されました。
各微分と勾配の概念について、その泛関数解析と非滑らか幾何学の観点から帰納し、それらの間の内在的な関係と数学的本質を確立するためのものです。
神がイスラエルに語られた言葉は私たちにも適用されます。「それゆえ、あなたがたがわたしの声に従い、わたしの契約を守るならば、あなたがたは地のすべての民の中で、わたしの宝となります。たとえば全地がわたしのものであるからです」(出エジプト記19:5)。
親愛なる者よ、これを覚えておいてください。「あなたがたは主、あなたがたの神の聖なる民であり、主はあなたがたを自分のために選び、地のすべての民の中で、特別な宝となるようにとあなたがたを選ばれたのです」(申命記14:2)。
デビッドウィルキンソン
今すぐ聴く
デビッド・ウィルカーソンによって
今すぐ聞く
親愛なる者よ、これを覚えておいてください。「あなたがたは主、あなたがたの神の聖なる民であり、主はあなたがたを自分のために選び、地のすべての民の中で、特別な宝となるようにとあなたがたを選ばれたのです」(申命記14:2)。
デビッドウィルキンソン
今すぐ聴く
デビッド・ウィルカーソンによって
今すぐ聞く
免責事項:このコミュニティは、Moomoo Technologies Inc.が教育目的でのみ提供するものです。
さらに詳しい情報
コメント
サインインコメントをする