Nikkei 225 futures and single option basic course Delta Edition 2-1 delta-neutral and straddle butterfly.

1. Delta Neutral and Straddle Butterfly

This time, I would like to explain the Delta Neutral strategy as part of the basics course on Nikkei 225 Futures and Options, Delta Edition 2.
We will introduce specific strategies such as Straddle, Butterfly, Strangle, and Condor, and explain how to neutralize Delta using Nikkei 225 mini as a more common combination. Let's take a look at what this is all about.

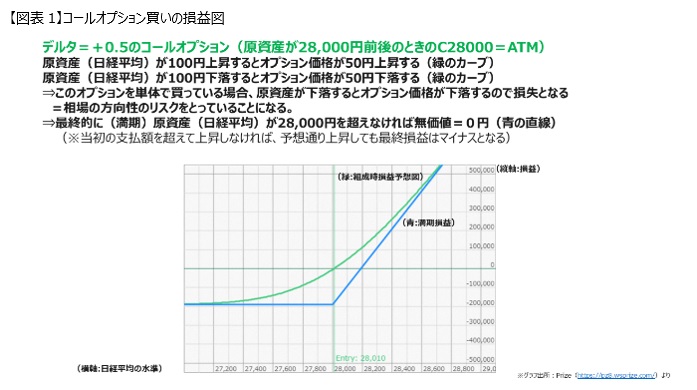
Considering the Call Option with Delta +0.5 when the underlying asset (Nikkei Average) is around 28,000 yen for C28000.
Since the underlying asset is an option close to the exercise price, it was At The Money (ATM).
With a Delta of +0.5, theoretically, when the Nikkei Average rises by 100 yen, the option price increases by 50 yen, and when the Nikkei Average falls by 100 yen, the option price decreases by 50 yen.
The green curve in [Figure 1] above is the expected profit and loss diagram at the moment of buying a Call Option, representing how the profit and loss unfolds.

If you buy this Call Option individually, as calculated now, if the underlying asset falls, the value of this Call Option decreases, resulting in losses.
If you buy this call option, you are taking directional risk.

If the market goes up, you will make a profit, and if it goes down, you will incur a loss.
By looking at this blue graph, if it does not exceed 28,000 yen at maturity, it will result in a loss and become worthless. Even if it rises slightly, if it does not exceed the initial payment amount, the final profit and loss will be negative.

In other words, the market must rise above the breakeven point.

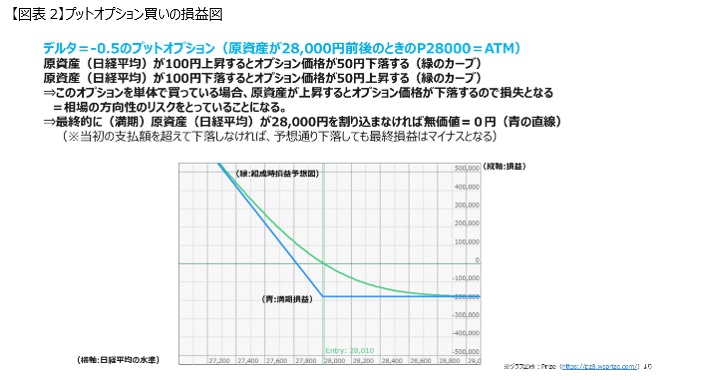
While profit and loss outcomes are often explained using call options, let's also take a look at put options in [Figure 2].
Put options are designed to increase in price when the underlying asset falls.
The delta value is in the form of -0.5, with a negative sign. It is easier to understand if you think of it as the reverse of a call option.

In other words, if the underlying asset increases by 100 yen, the price of the put option will decrease by 50 yen. If the underlying asset decreases by 100 yen, the price of the put option will increase by 50 yen.

In the world of Nikkei 225 options, they are traded at 1,000 times, so it can be understood that changes in option prices of around 0.05 million yen occur.
If you are buying this put option individually, when the underlying asset rises, the option price falls, resulting in a loss, exactly taking directional risk in the market.
If the underlying asset does not fall below ¥28,000, it will become worthless, and you will lose all the amount you initially paid.
If it falls below ¥28,000, you can recover some, but if the underlying asset does not drop below the breakeven point, the final profit and loss will end up negative.

Considering both call options, which increase in value when the underlying asset rises, and put options, which increase in value when the underlying asset falls, is the initial focus of this discussion.

As seen earlier, a call option with a delta of +0.5 will result in unlimited profits if the Nikkei average continues to rise above the breakeven point.
On the other hand, when the Nikkei average falls, it will limit the loss in a certain amount as it bends at ¥28,000, but in the case of a put option, there is a possibility of infinite profits when the Nikkei average falls, while losses will be capped at the initial payment if the Nikkei average rises.

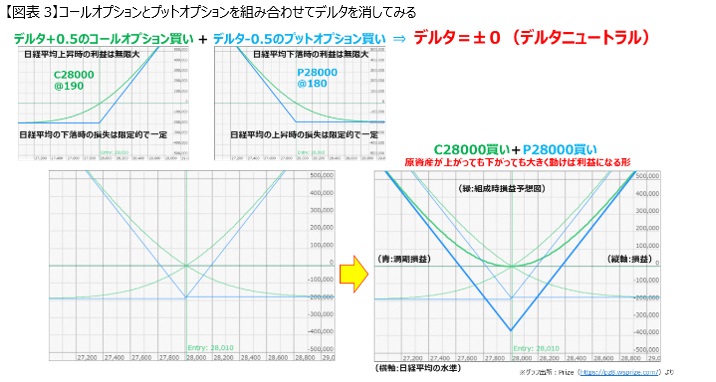
Therefore, combining the two will result in a V-shaped profit and loss graph as mentioned above.
If the market rises, the put option will reach a certain loss halfway through, so in the end, profit will come from the call option. If it falls, the value of the put option will become infinite, but the loss of the call option will become constant from halfway, so if it falls more than a certain amount, the profit will increase.

As explained in the expiration profit and loss diagram, options reach a constant loss at the bent point, which means that you will not lose more than the amount you initially paid. On the other hand, if the direction is correct, the option price will increase at the same rate as the rise or fall of the underlying asset, creating a V-shaped graph.

Buying and selling futures will result in neither losses nor profits, but with options, if you buy both C28000 and P28000 simultaneously, it will create this V-shape. Therefore, there is a possibility of making a profit if the market rises significantly or falls significantly.

By avoiding directional risk, that is, by neutralizing the delta, the direction of the underlying asset becomes irrelevant, and it becomes a battle of whether the market moves beyond the amount paid for the option, regardless of the direction of the market movement.

Illustrating this is the V-shaped graph in [Figure 3].

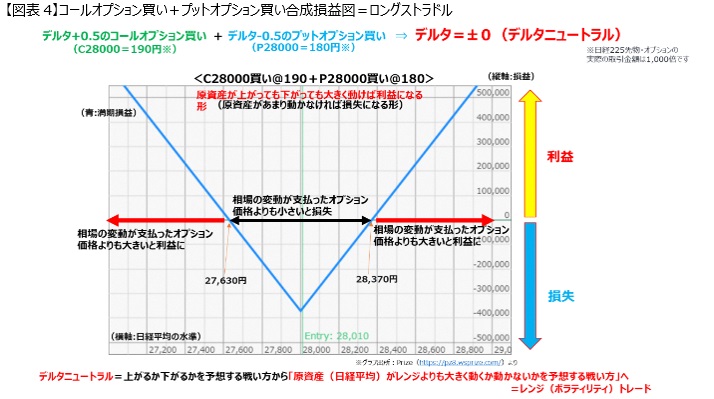
The above [Figure 4] is a diagram that extracts only the final appearance of the combined graph mentioned earlier.
In a scene where C28000 was bought at 190 yen and P28000 was bought at 180 yen, totaling 370 yen; it is exactly 370 yen above and below the ATM 28,000 yen, which is the breakeven point.
If the market rises above the amount you paid, or if it falls, there is a potential for profit.

Ultimately, by becoming delta neutral, what we are doing is changing the way we take risks from predicting whether it will go up or down to predicting whether the Nikkei average will move significantly more or not from a certain range.
The range of the market, in other words, the variability (ratio) of the underlying asset, also known as volatility, and this variability (ratio) is volatility. The above strategy changes the way of risk-taking based on the final (real) volatility, if you think the final volatility is higher than the volatility indicated by the option price, you should buy it, and if you think it won't move much, you should sell it. That's how you can adopt such a strategy.

This is a way of fighting that cannot be achieved simply by selling or buying regular stocks, or by selling or buying futures.

In this way, breaking away from whether the market will rise or fall, the direction is not relevant anymore, because it has changed to a battle of whether the stock price volatility will move more than the option's paid amount, or stay within it.
Still, the prediction of whether it will move or not must be realized.

In that case, as you can see from the profit and loss graph, since you are paying 190 yen and 180 yen, if it stops exactly at 28,000 yen, you will lose 0.37 million yen, 370 yen x 1,000 times.
If there is an increase or decrease of about 370 yen, it will be ±0.
Certainly, if this increase is remarkable, or if there is a huge crash, it will result in unlimited profit. However, in this case, a considerable increase or decrease is necessary, and since unlimited rising or falling is not common, you can consider it good enough if you cannot bear this loss yourself.

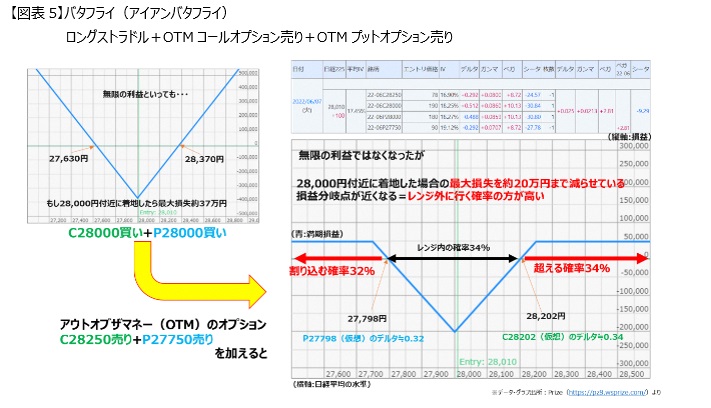
So, by buying C28000 and P28000, selling the C28250 outside by about 250 yen as an OTM option, and selling the P27750 about 250 yen outside, you can create a position where you give up the infinite rise of the graph and also stabilize the profit.

Because the shape of this [Figure 5] graph resembles a flying butterfly, it is called a butterfly.
A strategy using both call and put options to achieve this is specifically called an Iron Butterfly.

As selling occurs, it is evident that the maximum loss can be reduced from 0.37 million yen to about 0.2 million yen. However, the profit when it rises has decreased to about 0.05 million yen.

From the perspective of the delta definition of the probability of reaching, in terms of this profit and loss breakeven point section, the breakeven point is 28,202 yen on the upper side and 27,798 yen on the lower side.
The profit and loss breakeven point can be determined by adding or subtracting the prices of the call and put options from 28,000 yen. For example, if there is a call at 28,202 yen, the delta would be around +0.34, meaning it can be considered to have a 34% probability of reaching it.

Alternatively, if there is an option at 27,798 yen, the delta would be around +0.32, indicating that there is about a 32% probability of falling below this 27,798 yen, according to the definition of delta.

This means that the probability of fitting within this range is 34%, while the total probability of going outside is 66%. Therefore, whether this strategy works or not is something you can consider by looking at the probabilities yourself. If in pricing the option it is 34%, but you believe that the probability of going further outside should be higher, and the probability of fitting inside should be lower, then you should take this position.

In the battle of whether to stay inside the range or go outside, this time, it is good to achieve a position staying inside the range by selling options.
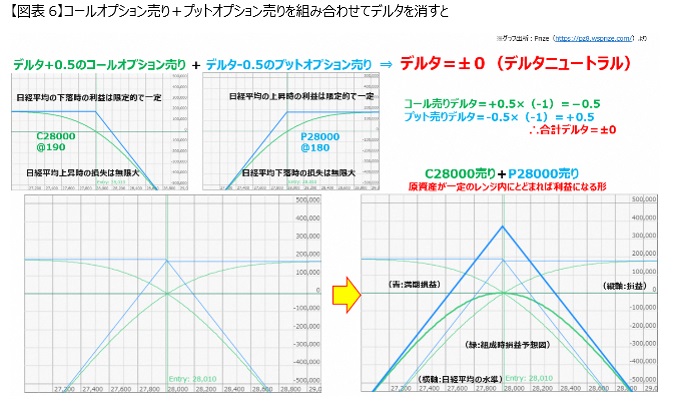
Selling the C28000 with Delta +0.5 results in a graph like the one in Figure 6, top left.

In other words, if it falls, the full profit is the 190 yen received, but if it rises, it becomes the opposite graph of buying options, with infinite losses.
On the other hand, selling P28000 with Delta -0.5 results in the opposite of the previous put option buying, and if it reverses up and down, the value of the put option becomes 0, so it is fixed at 180 yen (0.18 million yen).

However, in the case of a decline, the loss will expand infinitely, as it is the opposite of buying. (Top right graph). By combining these options, the total delta becomes ±0, creating a delta-neutral position. It is the opposite of the buying strategy, forming a mountain-shaped graph. As for profit and loss, (profit is above the 0 line), if the underlying asset stays within a certain range, ultimately it will result in a profit.

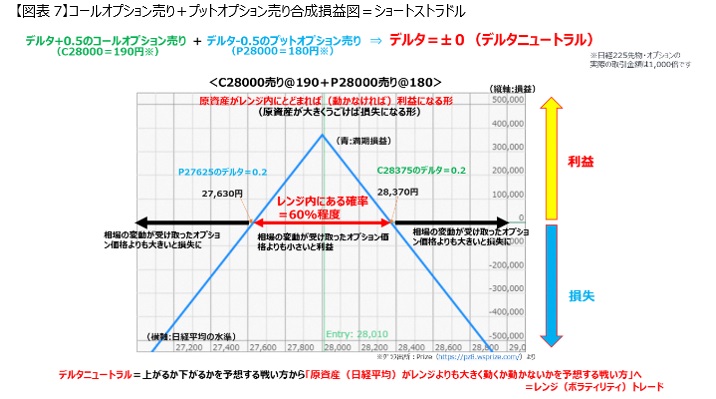
The break-even point of this position was exactly 370 yen, so it is right in the middle, 370 yen above and 370 yen below. If it stays within this range, there will be a profit. If it moves beyond that, it will result in a loss.
And as the movement becomes larger, the position will incur increasing losses. Looking at the deltas near the breakeven point (around C28375 or P27625), they are roughly around ±0.2. Since there is a 20% probability of moving outside, it can be said that the probability of staying within the range is about 60%.
In terms of probability, the probability of staying inside is high, and considering the current market environment to be sluggish, one can aim to take such a position to try to stay inside.
However, while the win rate is certainly high at 60%, it would be catastrophic if a major crash were to occur.

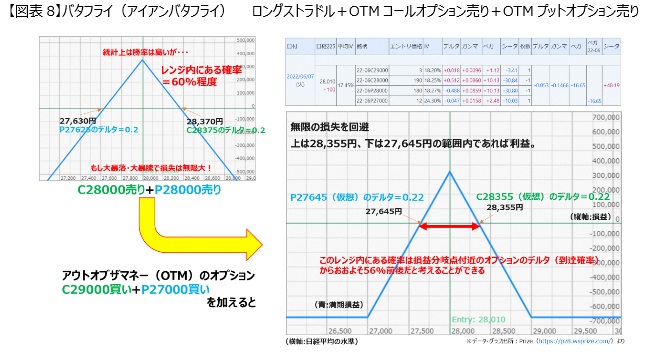
Although the probability of fitting within the range is high, it can lead to significant losses in the event of a sharp rise or a major crash, so consider taking a position that involves buying options on the outside as insurance.
For example, buy a call option at 29,000 yen, which is exactly in the middle (ATM) and deviates by 1,000 yen, and also buy a put option at 27,000 yen.
This will result in the graph as shown above.
Creating a scenario where the top of the mountain is in the middle, with maximum losses fixed on the right and left sides, can help prevent unlimited losses and provide some peace of mind.
Since the risk is lower than that of the earlier short straddle, the win rate decreases.
As payments are required due to making purchases, the breakeven points are closer. The upper point is at 28,355 yen, and the lower point is at 27,645 yen, with a slightly narrower profit range.
Considering from a delta perspective, there is about a 56% chance of making a profit.

This is a strategy to execute when you think the market will not move, and you want to fix your losses to a certain extent even if your financial estimates turn out to be wrong.
This profit and loss diagram looks like a butterfly shape (the central part is the body itself, and the part with constant losses on the left and right is like wings), so it is called a butterfly.