How to Balance the Risk and Reward of an Option Strategy?

To successfully trade options, it's crucial to strike a balance between risk and reward.

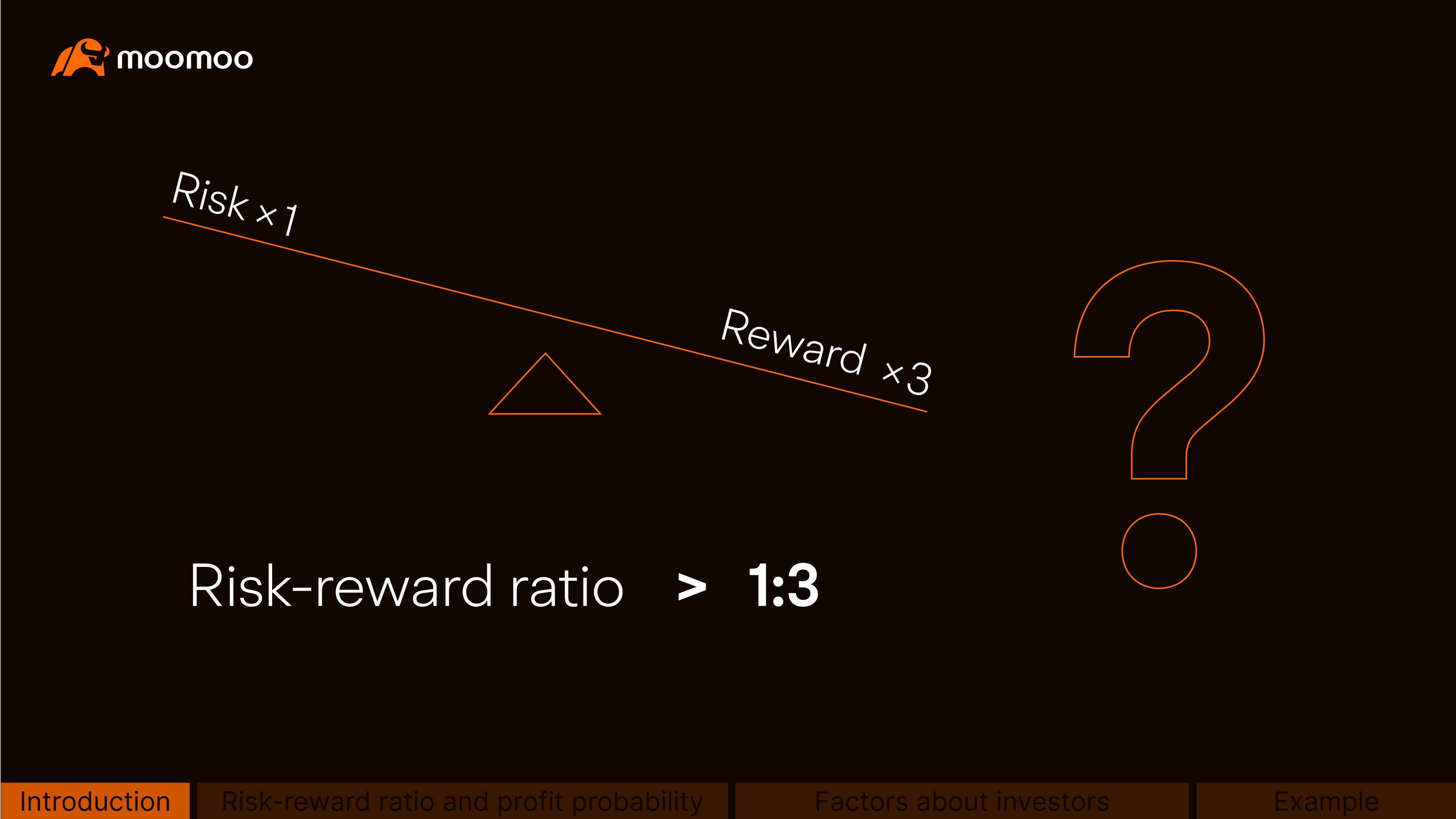
One commonly used indicator is the "risk-reward ratio," which some think should be at least 1:3.

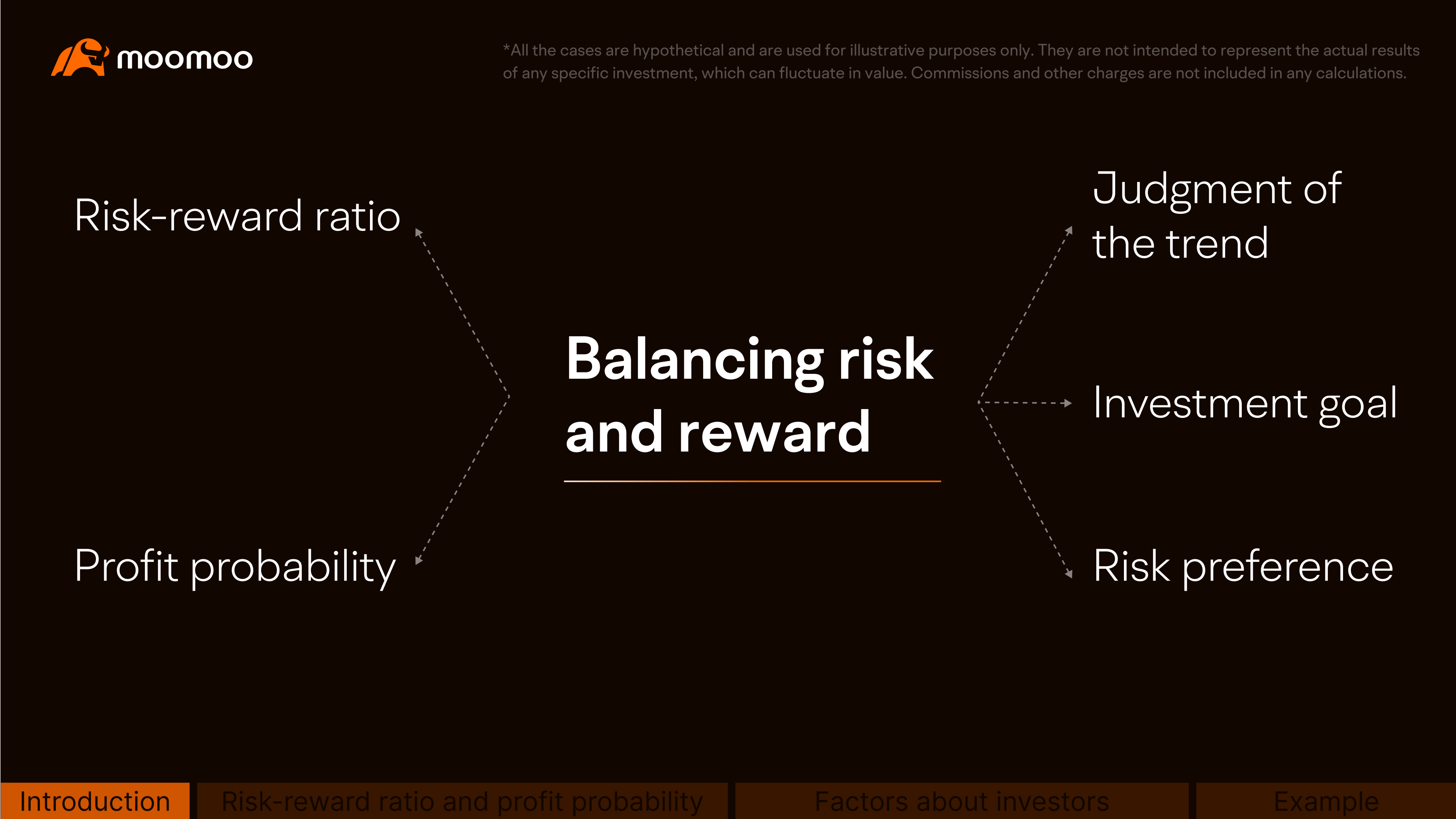
While the risk-reward ratio can be helpful, other factors, such as probability, must also be considered, such as judgment of the trend, investment goal, risk preference and other personal factors.

Let's take a closer look.

(Note: All the cases are hypothetical and are used for illustrative purposes only. They are not intended to represent the actual results of any specific investment, which can fluctuate in value. Commissions and other charges are not included in any calculations.)

First, what is the risk-reward ratio?

In options trading, it typically refers to the ratio of the maximum potential loss to the maximum potential profit.

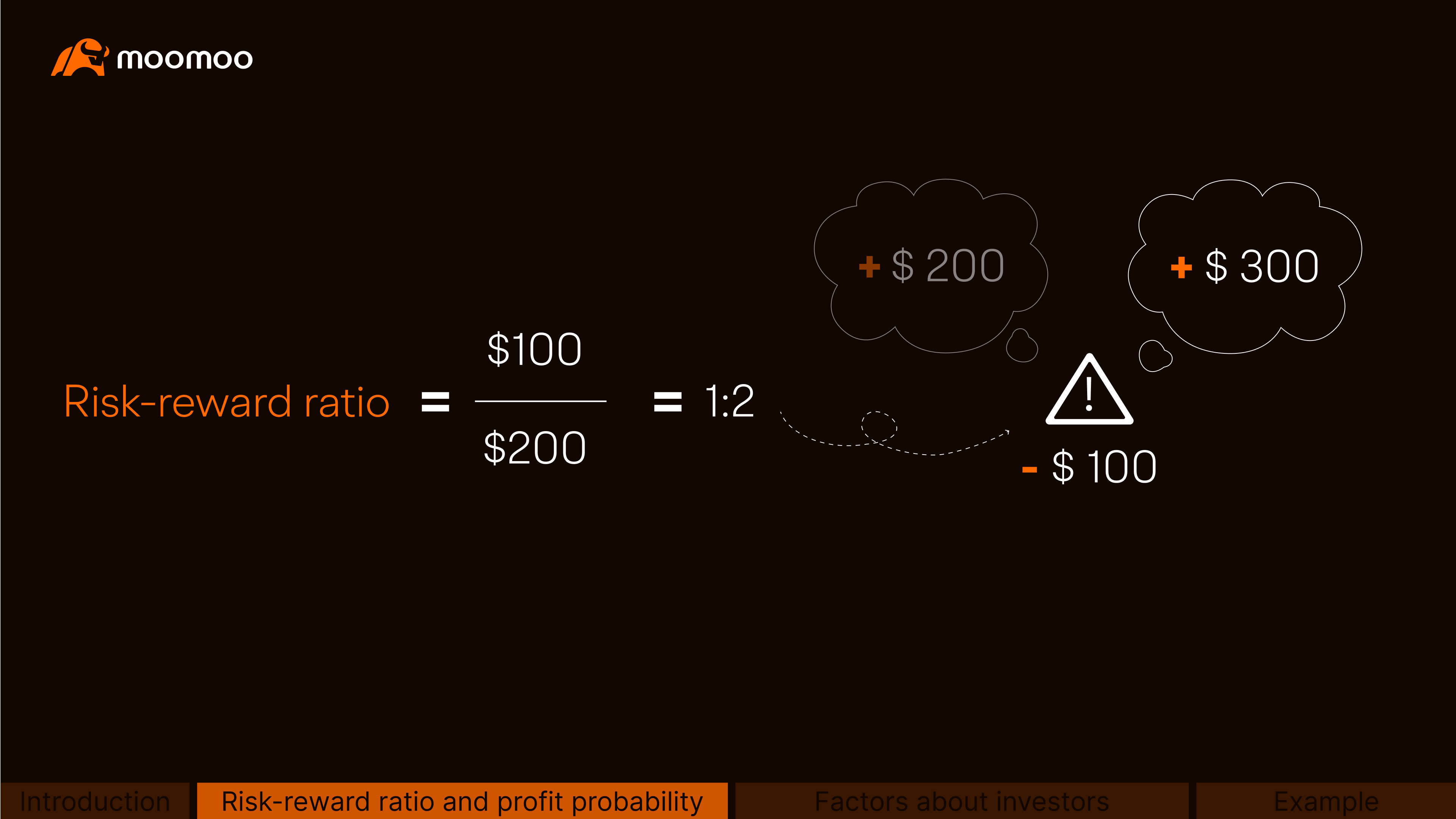
For example, if an option strategy has a maximum potential loss of $100 and a maximum potential profit of $200 at expiration, its risk-reward ratio would be 1:2.

In other words, investors using this strategy are willing to take on the risk of losing $100 to potentially gain $200, while a risk-reward ratio of 1:3 means risking $100 to potentially make $300.

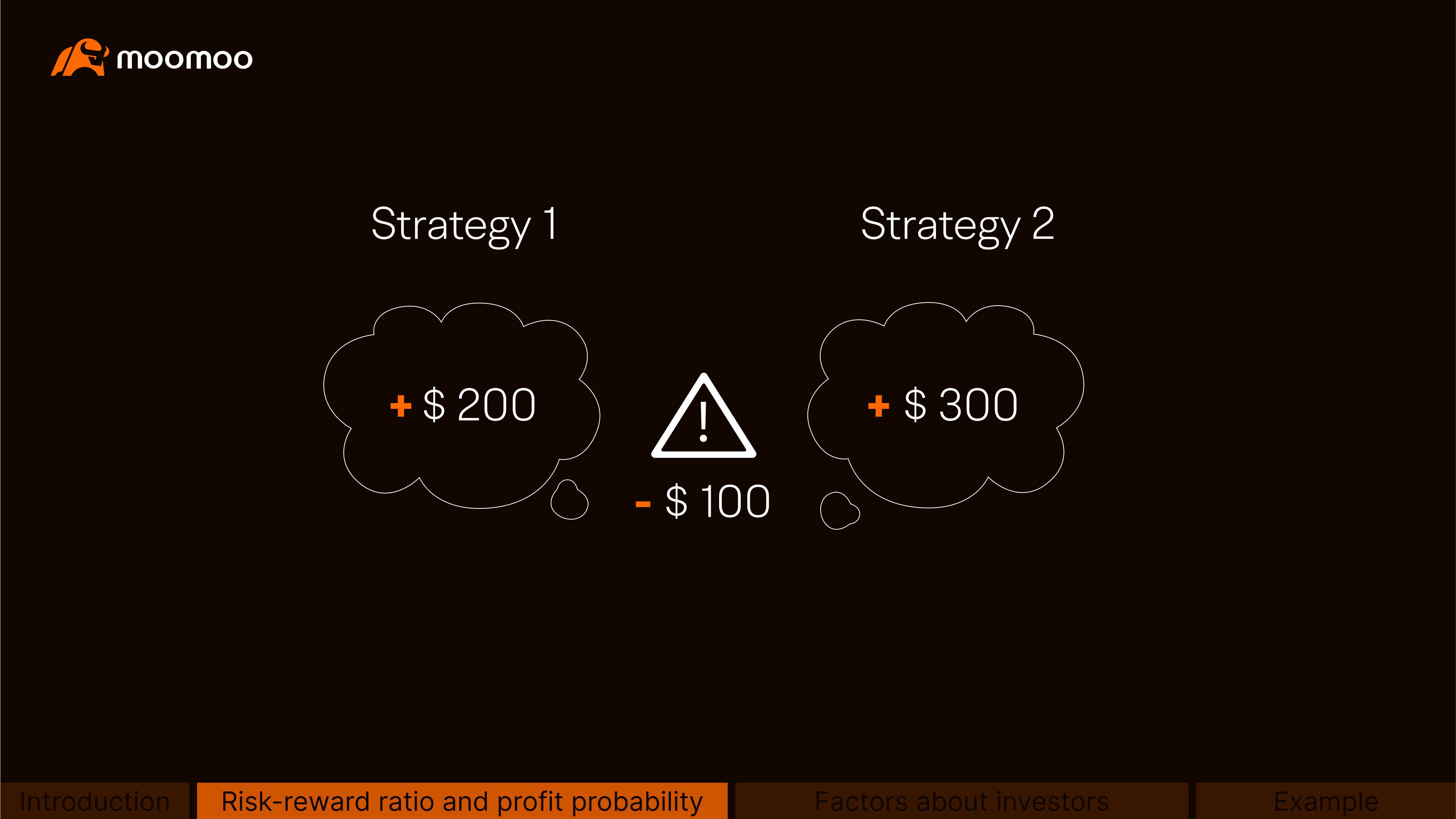
Is the risk-reward ratio the only essential factor in choosing a strategy? Let's consider two scenarios:

Suppose Strategy 1 is expected to have a risk-reward ratio of 1:2, and there's a 70% probability of realizing the maximum profit of $200, while the $100 maximum loss is 30% likely.

On the other hand, Strategy 2 has a risk-reward ratio of 1:3, and there's a 30% probability of realizing the maximum profit of $300, while the $100 maximum loss is 70% likely.

Let's assume an investor makes ten trades using each strategy, and the results fully comply with the law of probability. We will get:

When using Strategy 1, the investor wins $200 seven times and loses $100 three times. The net gain will be $200*7 - $100*3 = $1,100.

Similarly, with Strategy 2, the investor wins $300 three times but loses $100 seven times. The net gain will be $300*3 - $100 *7 = $200.

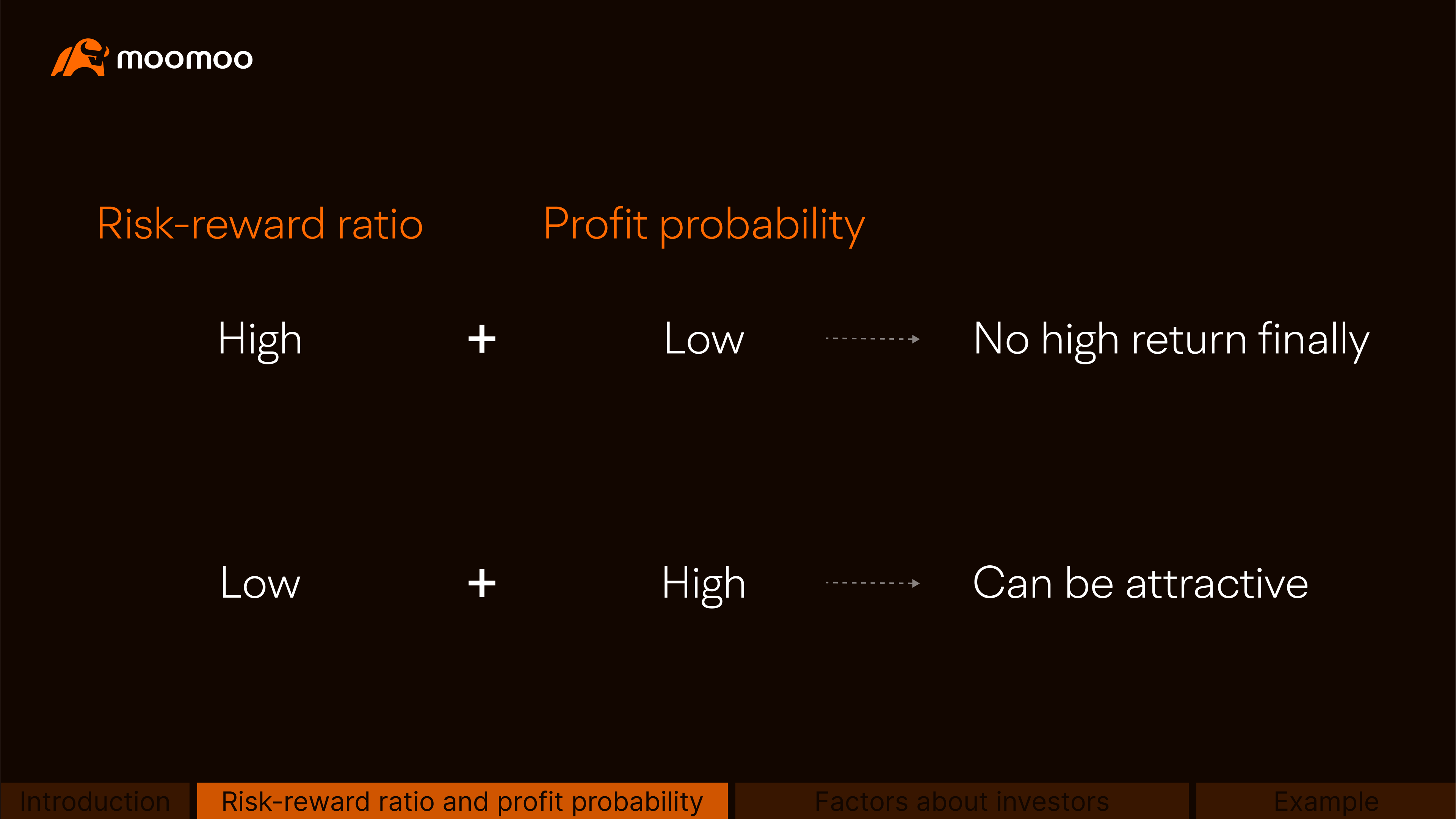
This example tells us probabilities for maximum loss and maximum gain also matter to the ultimate investment return.

If a strategy has a favorable risk-reward ratio but a low probability of success, the expected high return might not be realized.

Conversely, a strategy with a poor risk-reward ratio but a high profit probability can still be potentially attractive.

In options trading, the profit probability boils down to a trader's judgment.

For instance, the profit probability for the long call strategy is based on the success rate of expecting the underlying stock price rising above the strike price by expiration.

If you are not good at judging the underlying stock price trend, the likelihood of realizing gains will be very low.

Now let's move on to look at other influencing factors of return, which have a lot to do with investors themselves.

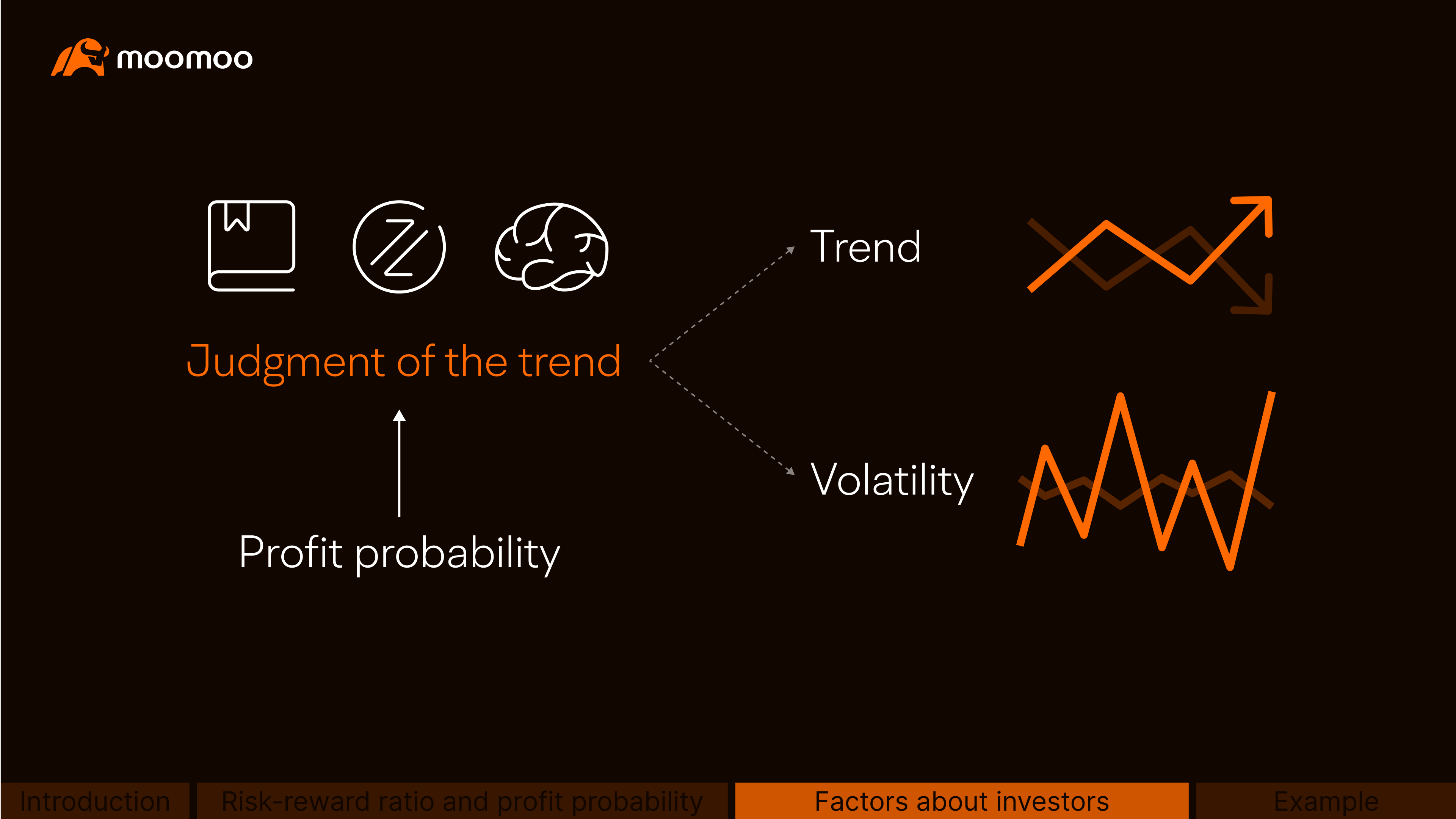
First, investors' judgment of the market trend.

This can involve predicting when and how much the underlying asset will rise or fall, or the underlying asset's volatility in a specific period.

As we've mentioned earlier, the success rate of investors' judgment actually affects the profit probability of their strategy. As a result, investors need to have a sharper eye on the market, which requires them to strengthen their financial knowledge, hone their investing skills, and think deeper.

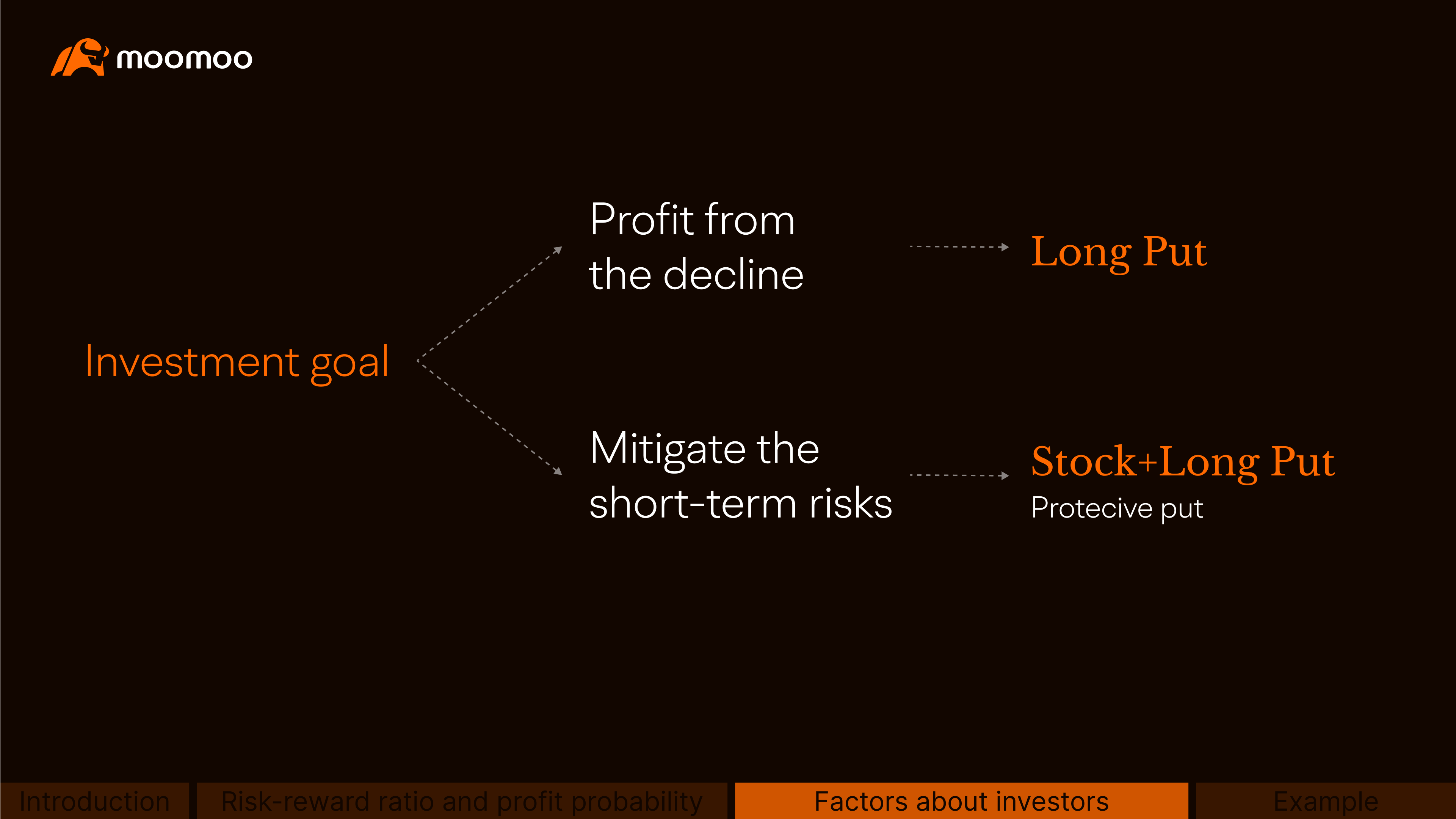
Second, investment goals also play a role.

Suppose there are two investors both thinking that the price of stock Y will decline in the short term.

One investor may seek to profit from the decline by using a long put, a single-leg strategy. The other investor may choose to mitigate the short-term risks associated with the decline while still holding the stock by using a protective put.

Third, investors' risk preference may also impact their decisions.

Likewise, let's suppose both investor A and investor B believe that the price of stock Y has a 70% probability to rise above a certain price level in the short term and want to profit from it.

Assume investor A can tolerate the remaining 30% probability of stock Y trading below the price level, while investor B feels extremely anxious about it.

As a result, investor A may buy a call only, while investor B may opt to sell another call option with a higher strike price besides buying the same call as investor A to lower the overall cost, which is called a bull call spread.

Let's take a look at an example of how the above factors come into play when balancing risk and reward.

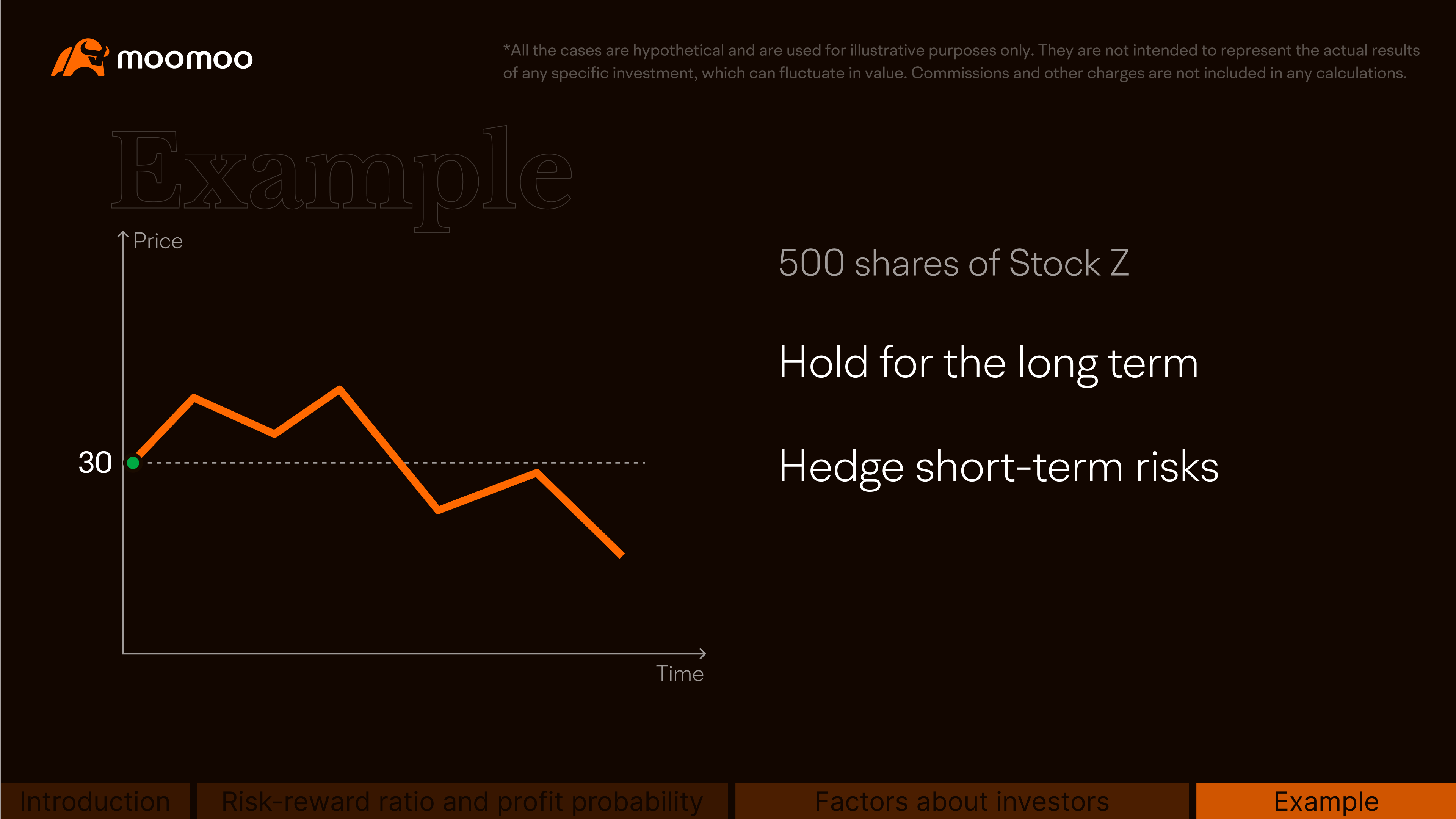
Suppose stock Z is trading at $30, and Jack holds 500 shares.

He wants to hold the stock for the long term but expects that the stock price may fall in the short term.

He is willing to pay a premium to hedge short-term downside risks.

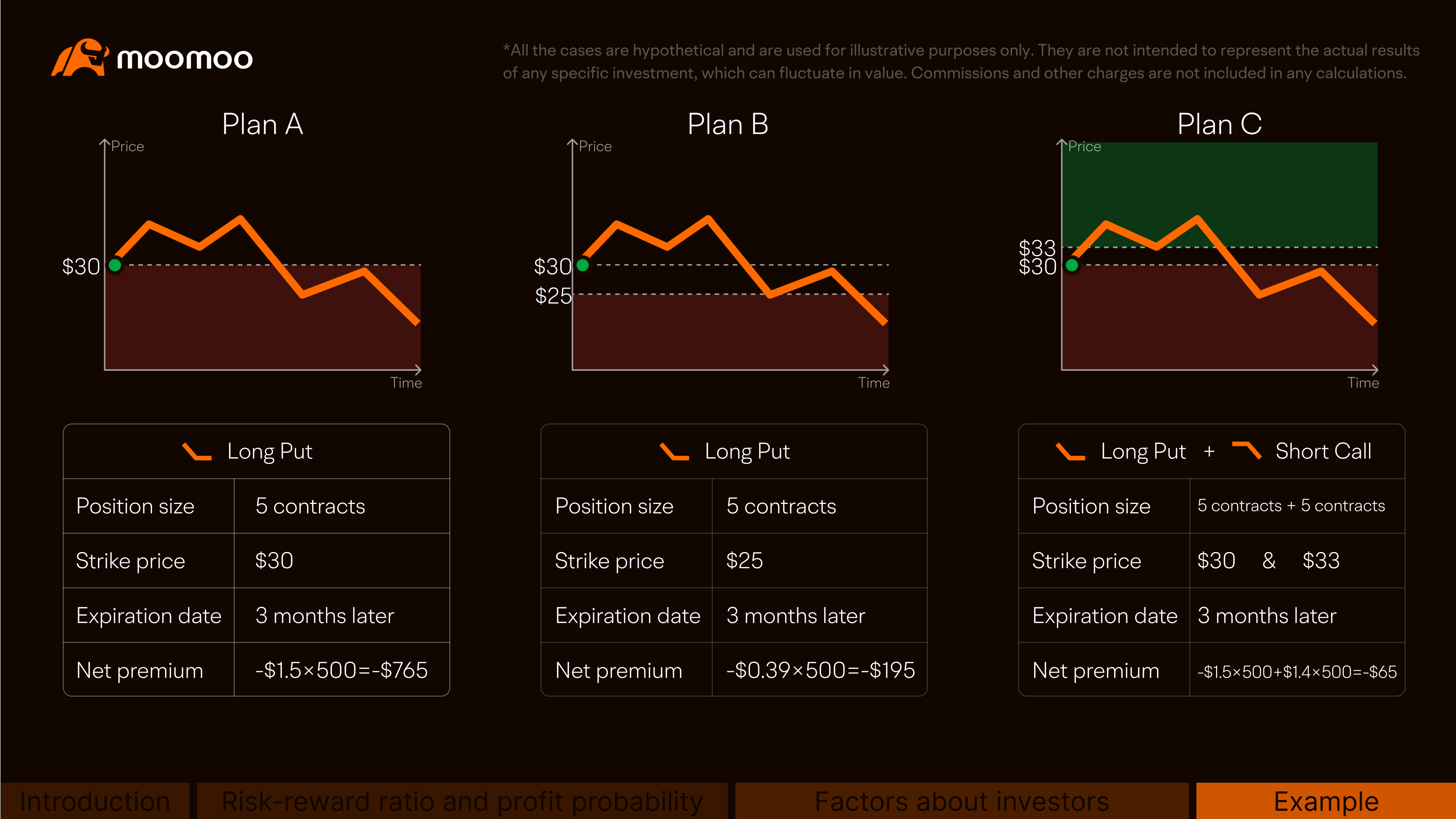
He can structure his option strategy in different ways, and each of them has its distinct risk and reward profile.

Plan A is to cover all the downside risks by expiration. Jack considers buying five American-style puts at $1.5 per share with a strike price of $30 that expires in three months with a total cost of $1.5*500 = $750.

Plan B is to cover the downside risks partially (when the stock falls below $25) by expiration. He buys five American-style puts at $0.39 per share with a strike price of $25 that expires in three months with a total cost of $0.39*500 = $195.

Plan C is to cover all the downside risks by expiration and reduce the initial cost.

He buys five American-style puts at $1.5 per share with a strike price of $30 that expires in three months, paying $1.5*500 = $750.

Second, as he believes the stock price will not rise more than 10% during this period, he sells five American-style calls for $1.4 per share with a strike price of $33 that expires on the same date. He earns a premium of $1.4*500 = $700 in total.

His initial net cost is only $50, but a potentially higher profit will be sacrificed if the stock price rises more than 10%.

Let's compare the risk-reward ratios of these three plans and their profit probability.

If the chance of the stock trading above or below $30 is 50-50 by expiration, plans A and C have a 50% profit probability, while that of plan B is less than 50%.

As for the risk-reward ratio, let's consider the extreme case where the stock price can drop to zero, and the ratio is calculated on the expiration date because that's more straightforward.

If Jack executes Plan A, he spends $750 to buy the puts, which is his maximum potential loss, and when the stock price drops to zero, he can exercise the option and sell 500 shares at $30. But if he didn't buy the puts, his maximum possible loss would be $30*500=$15,000. Therefore, we see $15,000-$750 as Plan A's maximum potential profit.

Therefore, the risk-reward ratio for Plan A is 750:14,250, equal to 1:19.

Based on similar calculations, the risk-reward ratio for Plan B is 195:25*500-195, approximately 1:63.

As for Plan C, since it caps upside profit potential, which may be unlimited if not executing the plan, the losses this strategy sacrifices are unlimited in theory.

Thus, the risk-reward ratio of Plan C is not favorable, compared to the first two plans.

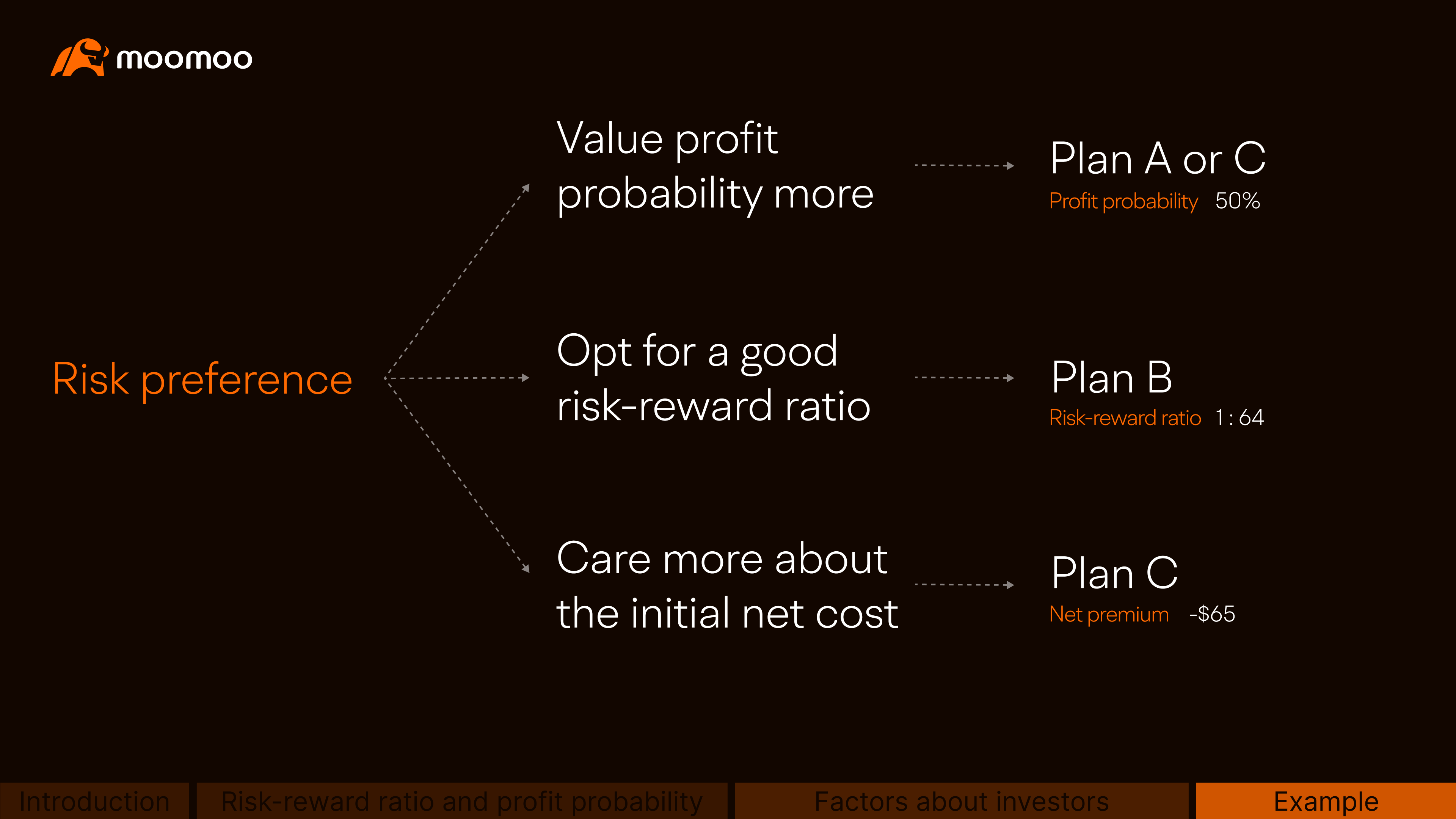
Having said all this, we have one more thing to consider, Jack's risk preference.

If he values profit probability more, he may choose Plan A or C, and pick Plan B if he opts for a good risk-reward ratio. If he cares more about the initial net cost, he may prefer Plan C.

In summary, when making an investment decision, investors should factor in a strategy's risk-reward ratio, profit probability, their own judgments, goals, and risk preferences.

And remember, except for the factors we've covered today about risk and reward, there are other factors, like the account's limitations.

Moreover, the prices of the underlying and its options change all the time after we set up a strategy.

So how to manage the risks management in the process? We may discuss it later.

We've covered a lot here. Do you have any ideas about balancing risk and reward of options strategies? Please share your thoughts with us in the Comments.