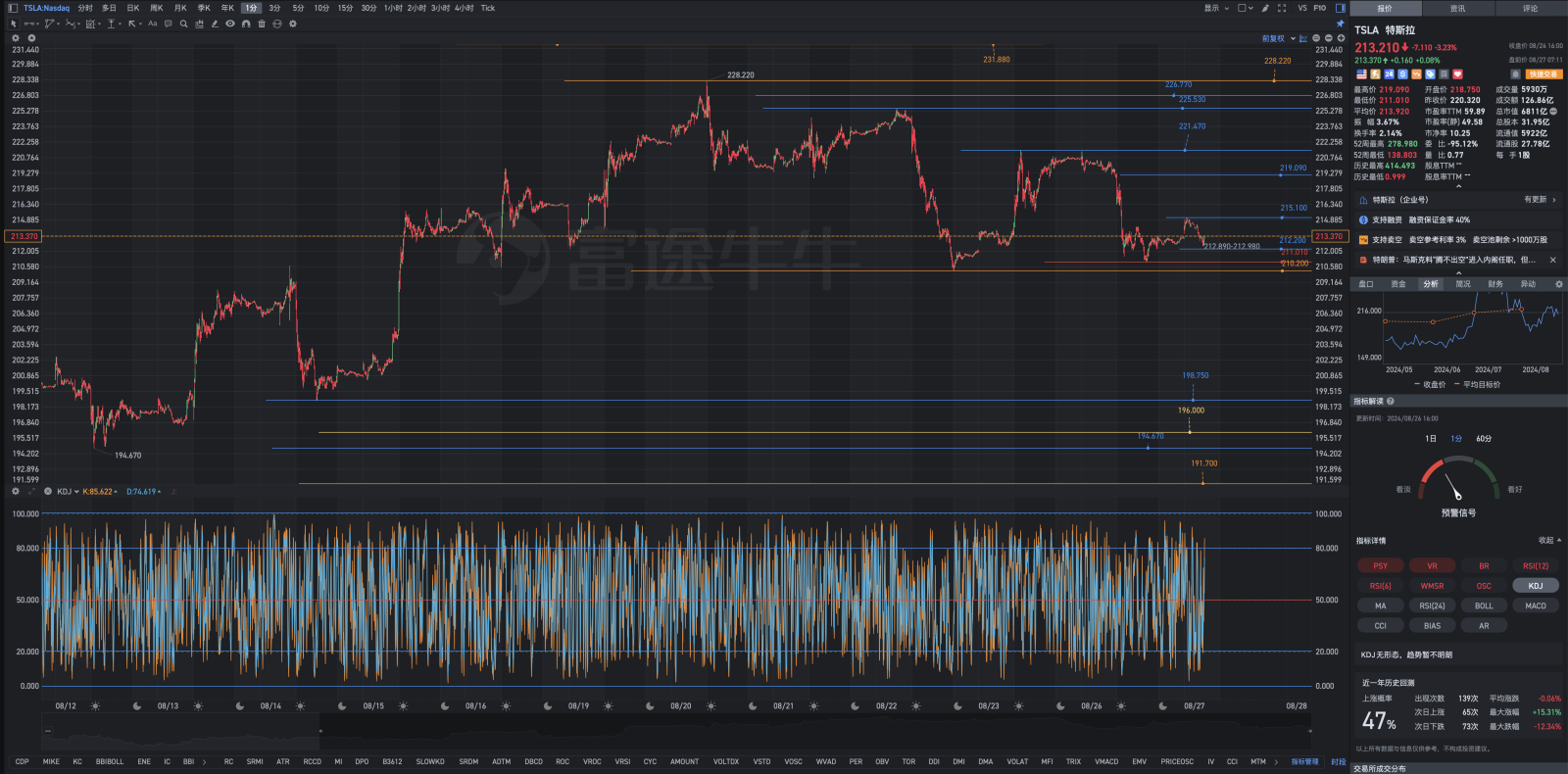
Tesla New York Pre-market Review Chart Analysis Formula
1. If the stock price rises, it is relatively simple. There are already a large number of long positions with floating profits waiting here. 60% of the positions are ready to be held long-term, there is no problem with impatience.
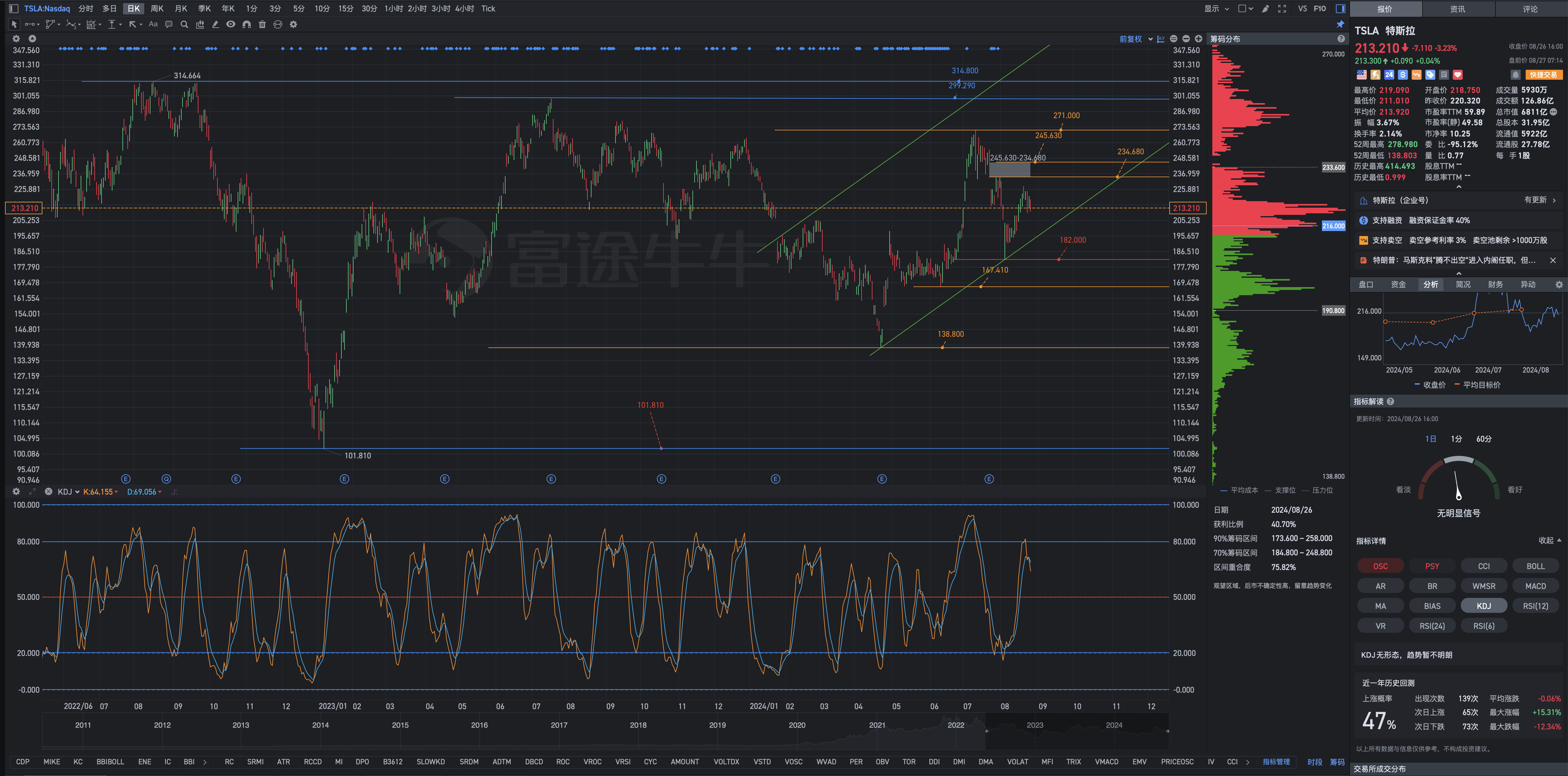
2. If the stock price falls, it is relatively more complicated. If the hourly KD indicator crosses below the 50 axis, and the corresponding daily KD indicator forms a death cross, then one should act accordingly, using a small amount of funds and positions for speculative trading.
3. If the stock price enters 211.100–210.200–182.000, it is necessary to use Tesla's Special funds for deep-fall re-buy: When Tesla's stock price enters the 211.100–210.200–182.000 range, there should be a planned and step-by-step approach, with a discrete random variable, to establish positions. It is not considered to build new long positions above 211.700 (the situation is different for those without long positions).
In principle, it is most ideal to establish positions when everyone is bearish on the market, unwilling to buy and hold, and afraid of the downturn and poor technical patterns and indicators, and the results have been good. Is there a need to do something in the 211.700–210.200 range? Undecided, those without long positions need to consider?
Vanguard (the world's largest asset management company) manages funds for individual retirement accounts (IRA) and 401(K) accounts in the United States, while State Street Global Advisors (the world's third-largest asset management company) are the two main players for Tesla stocks. They plan and execute in a systematic and stepped manner, using discrete random variables and a gradual approach to building positions. When building positions, they prefer quality over quantity and choose to buy stocks at a lower price rather than a higher price.
In the end, the consequences of being bullish or bearish and chasing highs or strength will show. Tesla's P/E ratio for the fiscal year 2024 has already reached 90 times, and the profit expectations for the fiscal years 2024 and 2025 have been continuously declining. With slightly over 60% of long positions, there is no need to be anxious about the rising stock price. However, going all-in or being overly defensive is a completely different story and not wise. A person without long-term planning or a focus on mental health in investment and trading will not go far. Even if Tesla has the potential to reach the range of 217,000-299,290-314,800, or even higher levels like 414,490-515,000, you won't be able to hold onto your floating profits.


Dear one, take a closer look at that scene, and you may see yourself in it. Have you ever spent a night of wailing and groaning because of the lies planted by the devil in your spirit? You may have cried out to God, "I've had enough; I can't take it anymore. This test is too difficult. The fortress in my heart will never crumble. I can never go on. I have lost this battle." - YouTube
Discussion of major unexpected events in financial markets (often represented as nonsmooth curves in mathematics) and the strategy of gradual and batch-based positioning in opening positions (often related to the generalized gradient problems and extremum problems of nonsmooth functions in mathematics):
Nonsmooth analysis is a development of convex analysis. The subdifferential theory of convex analysis enables people to generalize differential methods to handle extremum problems of nonsmooth convex functions. Nonsmooth analysis is devoted to the more general generalized differential methods for handling extremum problems of nonsmooth functions. The most successful example in this regard is the generalized gradient theory proposed by Clarke, F.H., for locally Lipschitz functions, which has become a classic work in this field since its publication in 1983, titled "Optimization and Nonsmooth Analysis". It establishes generalized differential calculus for mappings that are not differentiable in the classical sense. Convex analysis is the first step of nonsmooth analysis, and its foundational work belongs to Moreau, J.J. and Rockafellar, R.T.
It is a mathematical branch that studies convex sets and convex functions. Its main purpose is to use the convexity of sets and functions to deal with various analytical problems, especially extremum problems, including finite-dimensional mathematical programming problems and infinite-dimensional variational problems. Its main tools are the separation theorem for convex sets, subdifferential theory, and duality theory.
The concept of convex sets can be traced back to ancient Greece in the 3rd century BC. At that time, Archimedes had defined a convex arc as a plane curve where all the chords connecting points on it are on the same side. However, the systematic study of convex sets began with the work of German mathematician Minkowski, H., at the end of the 19th century and the beginning of the 20th century. Minkowski's interest in the study of convex sets arose from his research on "the geometry of numbers," such as the study of the number of integer points in a planar set. He proposed the concept of Minkowski function, which is now called the Minkowski function, to characterize the distance from a point to a convex set, which includes norm, seminorm, and other convex functions as special cases. In his posthumously published work in 1911, he proved the support theorem for convex sets in R. Afterwards, Carathéodory, C., and others further deepened the study of convex set theory, especially Carathéodory's theorem in 1911, which states that a convex set in R can be represented by n+1 points.
The systematic application of the concept of convex functions can be traced back to Cauchy, A.-L. The well-known Cauchy inequality, geometric mean less than or equal to arithmetic mean, etc., all originated from Cauchy's research on using the convexity of functions to prove inequalities. The systematic study of convex inequalities was the work of Jensen, J.L.W.V., who published a monograph on this topic in 1906. Inequalities used as definitions of convex functions are usually referred to as Jensen inequalities.
Helly, E., also made important contributions to early convexity theory. In 1917, he proved the Helly theorem, which states that if any n+1 sets in a compact convex set family in R have a non-empty intersection, then the entire family also has a non-empty intersection. As early as 1921, even earlier than Hahn, H., and Banach, S., he proved the Hahn-Banach theorem, which is a linear extension theorem for linear functionals involving convex functions and is equivalent to the support theorem or separation theorem of convex sets.
In the 1950s, the study of convexity became increasingly important due to the development of applied mathematical disciplines such as mathematical programming, game theory, mathematical economics, and optimal control, as well as the development of fundamental mathematical disciplines such as functional analysis, calculus of variations, and potential theory. In 1951, Fenchel, W. published the lecture notes 'Convex Cones, Convex Sets, and Convex Functions' at Princeton University in the USA, providing a systematic summary and development of the theory of convex sets, convex cones, and convex functions. In particular, he generalized the concept of the classical Legendre transformation in variational calculus to the now-called Legendre-Fenchel transformation or conjugate function, and introduced convenient new concepts such as supergraph and indicator functions. These have become fundamental concepts in convex analysis. Later, Klee, V.L. conducted an in-depth analysis of the theory of convex sets in a series of papers. Choquet, G. developed the Choquet-Minkowski theorem proposed in 1940 (compact convex sets are the closed convex hulls of their extremal points) and established the Choquet integral representation theory of compact convex sets and convex cones. The Browder fixed point theorem proposed in 1911 was also developed into various fixed point theorems for continuous mappings in compact convex sets during this period. Among them are the representative fixed point theorem for closed set-valued mappings in compact convex sets proposed by Kuratowski in 1941 and a series of minimal-maximal inequalities proposed by Fan (Ky Fan) from 1952 onwards.
Convex analysis is considered to be a relatively independent branch of mathematics, thanks to the work of Moreau, J.J. and Rockafellar, R.T. In 1967, Moreau's lecture notes 'Convex Functions' and Rockafellar's monograph 'Convex Analysis' published in 1969 were considered as the foundational works of convex analysis. In particular, the theory of subdifferentials and duality theory of convex functions made convex analysis a part of analysis as a whole. Moreau's lecture notes were presented in the framework of general locally convex topological linear spaces, while Rockafellar emphasized the applications in mathematical programming theory, limiting convex analysis to finite-dimensional spaces. Subsequently, Ekeland, I. and Temam, R. published 'Convex Analysis and Variational Problems' (1974) and other works on convex analysis in Banach spaces aimed at variational calculus, optimal control, and other applications.
After the 1970s, convex analysis further developed into nonconvex analysis, nonsmooth analysis, set-valued analysis, and so on. Many fundamental theorems of convex analysis have been extended to the case of nonconvex sets and nonconvex functions. The most notable is the generalized gradient theory of locally Lipschitz functions proposed by Clarke, F.H. in 1975. Since 1994, the first 'Journal of Convex Analysis' has been published internationally. According to the introduction of the journal, the generalized theory of convex analysis should include various generalizations of convex analysis, especially nonsmooth analysis and set-valued analysis.
Nonconvex analysis, which attempts to generalize the basic theory and methods of convex analysis to the case of nonconvex sets and nonconvex functions, is a branch of mathematics. This name is no longer commonly used today, and it has been replaced by nonsmooth analysis, set-valued analysis, etc.
Nonsmooth analysis is the development of convex analysis. The theory of subdifferentials of convex analysis allows for the extension of differential methods to handle extremal problems of nonsmooth convex functions. Nonsmooth analysis aims to establish a more general generalized differential method to handle extremal problems of nonsmooth functions. The most successful development in this regard is the generalized gradient theory proposed by Clarke, F.H. for locally Lipschitz functions. His book 'Optimization and Nonsmooth Analysis' published in 1983 has become a classic in this field.
Set-valued analysis is a branch of mathematical analysis that studies set-valued mappings. The concept of set-valued mappings has been present in mathematics for a long time. However, despite some limited research over the years, it was often considered unimportant. After the development of mathematical disciplines such as mathematical economics and mathematical programming theory in the 1950s, the concept of set-valued mappings played an essential role in these fields. For example, the demand mapping and supply mapping, which function as functions of price, are not single-valued; the stability of solution sets in mathematical programming problems also involves the continuity of set-valued mappings that depend on the parameter of the set of solutions (general mathematical programming problems do not have uniqueness of solutions). The generalization of the derivative concept in convex analysis, the subdifferential mapping, is also a set-valued mapping. Thus, a new branch called set-valued analysis gradually formed. In 1990, Aubin, J.P. and Frankowska, H. published the book 'Set-Valued Analysis', which preliminarily summarized the existing achievements in set-valued analysis. In 1994, the international 'Journal of Set-Valued Analysis' was published.
For each differential and gradient concept, they are summarized and summarized from the perspective of functional analysis and nonsmooth geometry in order to establish the inherent connection and mathematical essence between them.
The word that God spoke to Israel is for us today: “Now therefore, if you will indeed obey my voice and keep my covenant, then you shall be a special treasure to me above all people; for all the earth is mine” (Exodus 19:5).
Dear one, remember this: “For you are a holy people to the Lord your God, and the Lord has chosen you to be a people for himself, a special treasure above all the peoples who are on the face of the earth” (Deuteronomy 14:2).
Dear one, remember this: “For you are a holy people to the Lord your God, and the Lord has chosen you to be a people for himself, a special treasure above all the peoples who are on the face of the earth” (Deuteronomy 14:2).
Disclaimer: Community is offered by Moomoo Technologies Inc. and is for educational purposes only.
Read more
Comment
Sign in to post a comment