Riemannian geometry

In differential geometry, Riemannian geometry studies smooth manifolds equipped with Riemannian metrics, which are choices of positive definite quadratic forms on the tangent spaces of the manifold. It particularly focuses on angles, arc lengths, and volumes. By summing up each small part to obtain the overall quantity.
In the 19th century, Bernhard Riemann extended this concept.
Any smooth manifold allows a Riemannian metric and this additional structure aids in solving differential topological problems. It serves as an introduction to the complex structures of pseudo-Riemannian manifolds, most of which are the subject of four-dimensional studies in general relativity.
Riemannian geometry is related to the following topics:
Metric tensor
Riemannian manifold
Levi-Civita connection.
Curvature.
Curvature tensor.
Riemannian geometry was established by the German mathematician Riemann. In a paper he wrote in 1851 titled 'On the Hypotheses of Geometry,' he clearly proposed the existence of another geometry, opening up a new and vast field of geometry.
A fundamental rule in Riemannian geometry is that any two straight lines in the same plane have a common point (intersection). Riemannian geometry does not recognize the existence of parallel lines. Another postulate is that straight lines can be infinitely extended, but their total length is finite. The model of Riemannian geometry is a sphere that has been appropriately 'improved.'
Euclidean geometry, Lobachevskian geometry, and Riemannian geometry are three distinct geometries. Each of these geometries has a rigorous system of propositions based on its own axioms, satisfying harmony, completeness, and independence between the axioms. Therefore, these three geometries are all correct.
In our everyday space, which is neither too big nor too small, neither too far nor too close, Euclidean geometry is applicable; in the cosmic space or the world of atomic nuclei, Lobachevskian geometry is more in line with objective reality; in studying practical issues such as navigation and aviation on the surface of the Earth, Riemannian geometry is more accurate.
People finally realized the existence of a new geometry different from Euclidean geometry, known as non-Euclidean geometry. Shortly after, the German Riemann introduced another new axiom to replace the fifth postulate, creating another type of non-Euclidean geometry. Riemann's new axiom states, 'From a point outside a line, a parallel line cannot be drawn.' The mathematical community quickly recognized that these three geometries are all correct, reflecting the properties of spaces with different curvatures. The geometry created by Lobachevsky and Bolyai is called Lobachevskian geometry, while the geometry created by Riemann is called Riemannian geometry. Euclidean geometry is the geometry of flat space, Riemannian geometry is the geometry of positive curvature space, and Lobachevskian geometry is the geometry of negative curvature space.
In 1845, Riemann delivered his inaugural lecture titled 'On the Hypotheses Which Lie at the Foundations of Geometry' at the University of Göttingen, marking the birth of Riemannian geometry. Riemann unified these three geometries, collectively known as Riemannian geometry, and presented this work at the Department of Mathematics at the University of Göttingen in pursuit of a position as a lecturer.
Later, further refinement and expansion were carried out by E.B. Christoffel, L. Bianohi, C.G. Ricci, among others, making it a powerful mathematical tool for A. Einstein's creation of the general theory of relativity (1915). Subsequently, Riemannian geometry experienced vigorous development, especially by E. Cartan. His establishment of exterior differential forms and the moving frame method bridged the connection between Lie groups and Riemannian geometry, paving the way for extensive prospects in the profound development of Riemannian geometry, with far-reaching implications. In the past half-century, research in Riemannian geometry has evolved from local to global, yielding many profound results that play important roles in other branches of mathematics (such as algebraic topology, partial differential equations, several complex variables, etc.) and modern physics.
Riemann's research was based on Gauss's intrinsic differential geometry of surfaces. In Riemannian geometry, the most important type of object is the so-called constant curvature space. For three-dimensional space, there are three scenarios:
◆ The curvature is always equal to zero;
◆ The curvature is a negative constant;
◆ The curvature is a constant number.
Riemann pointed out that the first two scenarios correspond to Euclidean geometry and Lobachevsky geometry, respectively. The third scenario is Riemann's own creation, corresponding to another kind of non-Euclidean geometry. This third geometry denies the existence of 'parallel lines,' presenting a completely new non-Euclidean geometry, which is what is now known as Riemannian geometry in the narrow sense. It is the geometry with positive constant curvature, also known as spherical geometry, which was published in 1868, two years after Riemann's death.
Modern Riemannian geometry has found important applications in General Relativity. The spatial geometry in physicist Einstein's General Relativity is Riemannian geometry. In General Relativity, Einstein abandoned the notion of uniformity in time and space, believing that space-time is only approximately uniform in sufficiently small spaces, yet the entire space-time is not uniform. This interpretation in physics is remarkably similar to the concept of Riemannian geometry.
In addition, Riemannian geometry is also an important tool in mathematics. It is not only the foundation of differential geometry, but also applied in aspects like differential equations, calculus of variations, and complex function theory.



Complex analysis is the mathematical theory that studies functions of complex variables, especially analytic functions and meromorphic functions.
Common theories, formulas, and methods used in research include Cauchy's integral theorem, Cauchy's integral formula, residue theorem, Laurent series expansion, etc. The application of complex analysis is quite extensive and plays an important role in other branches of mathematics and physics, including number theory, applied mathematics, fluid dynamics, thermodynamics, and electrodynamics.
A complex function is a function where both the independent and dependent variables are complex numbers. More precisely, the range and domain of a complex function are both subsets of the complex plane. In complex analysis, the independent variable is also known as the "variable" of the function.
The Cauchy-Riemann equations in complex analysis, also known as the Cauchy-Riemann conditions, are two partial differential equations that provide necessary and sufficient conditions for a differentiable function to be holomorphic in an open set. They are named after Cauchy and Riemann. These equations first appeared in the works of Dirichlet, and later Euler related this equation system to analytic functions. Then Cauchy used these equations to develop his function theory. Riemann's paper on this function theory was published in 1851.

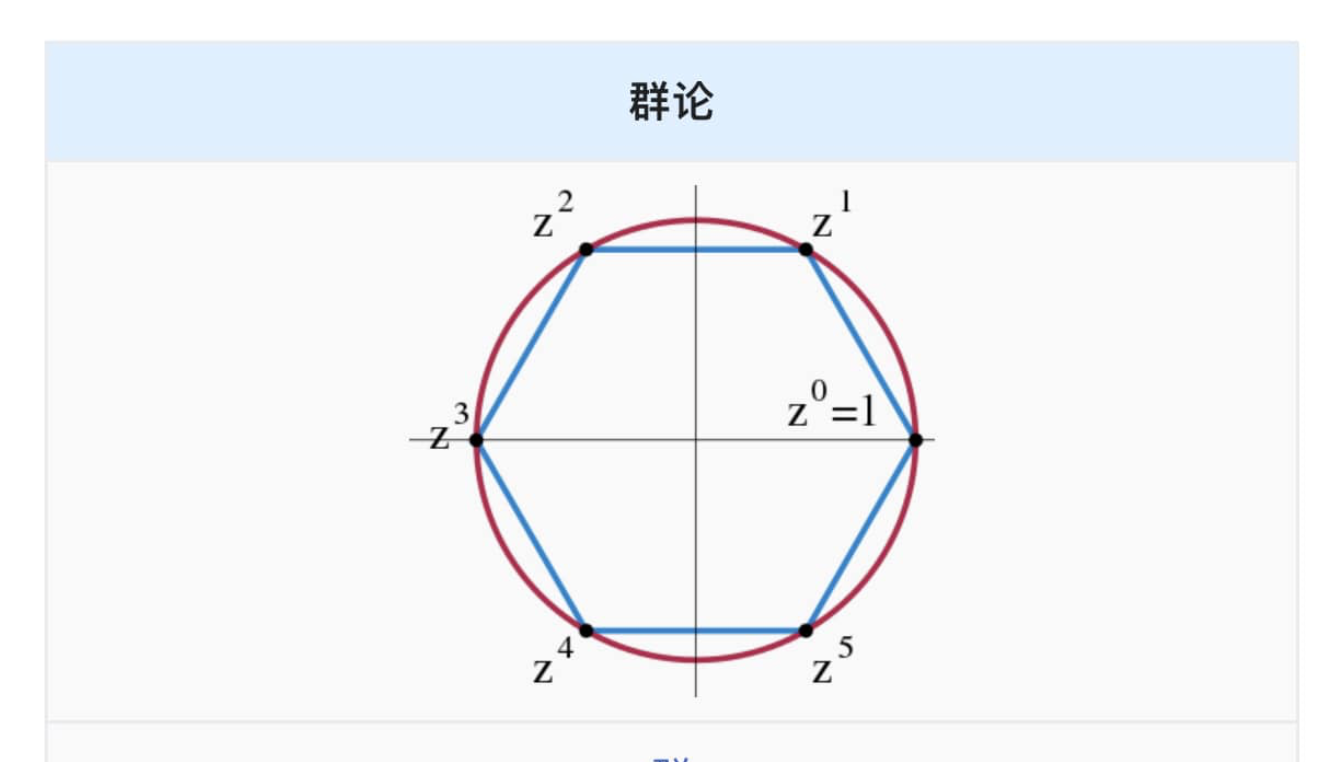
Groups have a fundamental and important position in abstract algebra: many algebraic structures, including rings, fields, and vector spaces, can be regarded as forming new operations and axioms on the basis of groups. The concept of groups appears in many branches of mathematics, and the research methods of group theory also have a significant impact on other branches of abstract algebra. Linear algebraic groups and Lie groups, as branches of group theory, have formed relatively independent research fields after undergoing significant development.
The importance of group theory is also reflected in the research of physics and chemistry, as many different physical structures, such as crystal structures and hydrogen atom structures, can be modeled using group theory methods. Therefore, group theory and related group representation theory have a wide range of applications in physics and chemistry.
An important result in group theory, the classification of finite simple groups, is one of the most important results in 20th-century mathematics. The proof of this theorem is the result of collective efforts and appears in journals published between 1960 and 1980, totaling over 10,000 pages.
The origins of group theory in history mainly come from three sources: number theory, algebraic equation theory, and geometry. The study of groups in number theory began with Leonhard Euler and was further developed by Carl Friedrich Gauss in the study of modular arithmetic and multiplication and addition related to quadratic fields. The concept of group theory was first implicitly used in algebraic number theory and later explicitly applied.
Early results on permutation groups appeared in the work of Joseph-Louis Lagrange, Paolo Ruffini, Niels Abel, and others on general solutions of high-degree equations. In 1830, Évariste Galois was the first to use the viewpoint of groups to determine the solvability of polynomial equations. Galois first used the term 'group' and established a connection between the emerging group theory and field theory. This theory is now called Galois theory. Arthur Cayley and Augustin Louis Cauchy further developed these studies and founded the theory of permutation groups.
The third major historical origin of group theory comes from geometry. Group theory first demonstrated its importance in projective geometry and played a role in subsequent non-Euclidean geometries. Felix Klein used the viewpoint of group theory to establish connections between different geometries, such as Euclidean geometry, hyperbolic geometry, and projective geometry, known as Erlangen Programme. In 1884, Sophus Lie began studying groups that appeared in problems of analysis (now called Lie groups).
The different origins from various fields led to different notations for groups. The theory of groups began to be unified around 1880. Since then, the influence of group theory has been expanding, and in the early 20th century, it promoted the establishment of abstract algebra, representation theory, and many other influential subfields. The classification of finite simple groups was a large-scale work in the mid-20th century, classifying all finite simple groups.
The types of groups considered in group theory have progressed from finite permutation groups and some special matrix groups to abstract groups. These abstract groups can be specified by generators and relations.
Group theory is widely used in mathematics, usually in the form of automorphism groups to reflect the internal symmetry of certain structures. Internal symmetry of structures often coexists with an invariant property. If there is an invariant in a set of operations, then the combinations of these operations and the invariant are collectively referred to as a symmetry group.
Abelian groups generalize the structures studied in other abstract sets, such as rings, fields, and modules.
In algebraic topology, groups are used to describe the invariant properties in topological space transformations, such as fundamental groups and covering groups.
The concept of Lie groups play a very important role in differential equations and manifolds, as they combine group theory and analysis to effectively describe symmetry in mathematical structures of analysis. The analysis of such groups is also known as harmonic analysis.
In combinatorial mathematics, abelian groups and group actions are commonly used to simplify calculations of elements in certain sets.
Later, group theory has been widely applied in various scientific fields. Wherever symmetry appears, its shadow will be present, such as in the physics superstring theory.
Disclaimer: Community is offered by Moomoo Technologies Inc. and is for educational purposes only.
Read more
Comment
Sign in to post a comment

Feinberg Investments : based analysis poster